Регистры сдвига с обратной связью

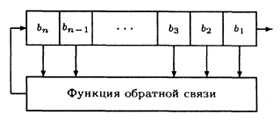
Большинство реальных поточных шифров основано на регистрах сдвига с обратной связью. Регистр сдвига применяют для генерации ключевой последовательности. Регистр сдвига с обратной связью состоит из двух частей: регистра сдвига и функции обратной связи.

Регистр сдвига представляет собой последовательность битов. (Количество битов определяется длиной сдвигового регистра. Если длина равна n битам, то регистр называется n-битовым регистром сдвига.) Всякий раз, когда нужно извлечь бит, все биты регистра сдвига сдвигаются вправо на 1 позицию. Новый крайний левый бит является функцией всех остальных битов регистра.

На выходе регистра оказывается один, обычно младший значащий бит. Периодом регистра называется длина получаемой последовательности до начала ее повторения.

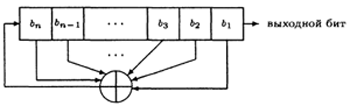
Простейшим видом регистра сдвига с обратной связью является регистр сдвига с линейной обратной связью (РСЛОС). Обратная связь представляет собой XOR некоторых битов регистра; эти биты называются отводной последовательностью.

РСЛОС (n-битовый) может находиться в одном из 2ⁿ−1 внутренних состояний. Это означает, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом 2ⁿ−1 битов. (Число внутренних состояний и период равны 2ⁿ−1, потому что заполнение РСЛОС нулями приведет к тому, что сдвиговый регистр будет выдавать бесконечную последовательность нулей, что абсолютно бесполезно.) Только при определенных отводных последовательностях РСЛОС циклически пройдет через все 2ⁿ−1 внутренних состояний. Такие РСЛОС имеют максимальный период. Получившийся pезультат называется М-последовательностью. Для того чтобы конкретный РСЛОС имел максимальный период, многочлен, ассоциированный с отводной последовательностью, должен быть примитивным по модулю 2 — то есть не раскладываться на произведение двоичных многочленов меньшей степени.

Например, многочлен x³² + x⁷ + x⁵ + x³ + x² + x + 1 примитивен по модулю 2. Рассмотрим этот многочлен в терминах РСЛОС с максимальным периодом. Степень многочлена задает длину РСЛОС. Свободный член многочлена всегда равен 1, и его можно опустить. Степени формальной переменной многочлена, за исключением 0-й, задают отводную последовательность, отсчитываемую от левого края сдвигового регистра. То есть члены многочлена с меньшей степенью соответствуют позициям, расположенным ближе к правому краю регистра. Тогда для взятого 32-битового сдвигового регистра новый бит генерируется с помощью XOR тридцать второго, седьмого, пятого, третьего, второго и первого битов; получающийся РСЛОС будет иметь максимальную длину, циклически проходя до повторения через 2³²−1 различных значений.

Сами по себе РСЛОС являются хорошими генераторами псевдослучайных последовательностей, но они обладают некоторыми нежелательными неслучайными свойствами. Для РСЛОС длины n внутреннее состояние представляет собой предыдущие n выходных битов генератора. Даже если схема обратной связи хранится в секрете, она может быть определена по 2n выходным битам генератора с помощью алгоритма Берлекэмпа-Мэсси.

Кроме того, большие случайные числа, генерируемые с использованием идущих подряд бит этой последовательности, сильно коррелированы и для некоторых типов приложений вовсе не являются случайными. Несмотря на это, РСЛОС часто используются при разработке алгоритмов шифрования.