Модели решения функциональных и вычислительных задач

(в нефтегазовом деле)

Для нефтегазового дела характерным является наличие огромного количества информации из разных источников, которую нужно быстро обрабатывать с помощью современных компьютерных средств, чтобы эффективно использовать.

Первым этапом получения информации является процесс измерения интересующих нас величин (примеры). Если наблюдаемая (измеряемая) величина распределена в пространстве (и/или во времени - примеры), то еще до начала измерений необходимо решить вопрос: сколько делать измерений по каждой координате, с каким шагом, с какой точностью измерять. Все эти вопросы рассматриваются в теории измерений, но и в информатике имеется похожая задача, которая возникает при оцифровке некоторых данных, заданных графически (или аналитически). Фундаментальное решение этой задаче сформулировано в теореме Шеннона-Котельникова. Предварительно рассмотрим пример оцифровки некоторой величины (сигнала), распределенной по одной координате.

Оцифровка

Сигнал, несущий информацию о некоторой измеряемой величине называетсяаналоговым,если он представлен в виде другой подобной ей величины (например, измеряемая величина высота представляется в виде отклонения стрелки прибора)

Сигнал, несущий информацию о некоторой измеряемой величине называется цифровым, если он представлен в виде последовательности чисел (или одного числа), отображающей значения наблюдаемой величины (например, та же высота, представленная в цифровом приборе)

Преобразование аналогового сигнала в цифровой сигнал называетсяоцифровкой

Пример

Рисунок 1. Пример аналогового сигнала

Во-первых, аналоговый сигнал (Рисунок 1) преобразуется в сигнал разделённый по времени, посредством периодической выборки (Рисунок 2). Временной интервал между двумя выборками называется периодом выборки, а его обратная величина называется частотой дискретизации. Согласнотеореме о дискретном представлении (теорема Шеннона-Котельникова), частота дискретизации должна быть, по крайней мере, в два раза больше наивысшей частоты сигнала. В противном случае такой сигнал не может быть однозначно восстановлен из выборки.

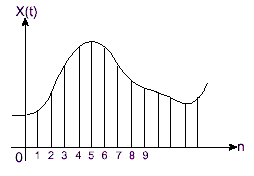
Рисунок 2. Временная дискретизация сигнала

Квантованием называется определение цифровых значений, соответствующих аналоговым выборкам, взятым на частоте дискретизации. Аналоговый сигнал квантуется путём приписывания аналоговой величине ближайшего «допустимого» цифрового значения (Рисунок 3). Количество цифровых значений называется разрешением и всегда ограничивается. Например, 256 значений для 8-битного цифрового сигнала или 10 значений в этом примере. Поэтому квантование аналоговых сигналов всегда приводит к потере информации. Эта ошибка квантования» обратно пропорциональна разрешению цифрового сигнала. Она также обратно пропорциональна динамическому диапазону сигнала, т.е. интервалу между минимальным и максимальным значениями (3 и 8 в этом примере).

Рисунок 3. Квантованный сигнал

На рисунке 4 показаны цифровые значения, которые соответствуют аналоговому сигналу. Эти значения сняты с выхода АЦП.

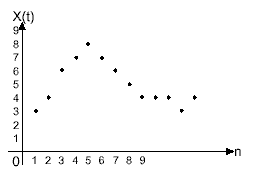
Рисунок 4. Цифровой сигнал

Итак, все необходимые величины измерены, данные оцифрованы и введены в компьютер.

Прежде чем начинать анализ данных и извлекать из них ценную информацию предстоит выявить и обработать погрешности, внесенные на этапе измерения и оцифровки.