Общие сведения о способах изображений - центральное и параллельное проецирование

Если между точкой S и плоскостью П' (пи-штрих) расположить точку А (рис, 1, а), провести прямую SA и найти точку пересечения этой прямой с плоскостью, то на плоскости П' появится изображение точки А или ее проекция А'. Процесс получения проекции точки пространства на плоскости называется проецированием. Плоскость П', на которую проецируют, называется плоскостью проекций, или картинной плоскостью. Прямые, с помощью которых получают проекции, называются проецирующими прямыми, или проецирующими лучами. Постоянная точка S, через которую проводят проецирующие лучи, называется центром проекций.

Предполагается, что в этой, точке находится глаз наблюдателя, когда он проецирует точку А на плоскость П'. Точку пересечения проецирующего луча с плоскостью проекций называют центральной проекцией точки. Такой вид проецирования называется центральным.

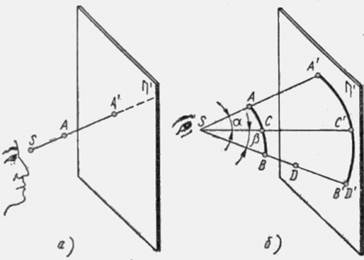
Рис. 1.

Если вместо точки взять кривую линию АВ, то для ее проецирования необходим ряд точек А, С, В (рис. 1, б). Проведя проецирующие лучи SA, SC и SB и найдя точки пересечения этих лучей с плоскостью проекций П', определяют проекции А', С' и В' точек А, С и В. Найденные проекции точек соединяют плавной кривой и получают проекцию А'С'В' кривой АСВ. Когда наблюдатель смотрит на кривую линию АСВ, она закрывает собой проекцию А'С'В'. Если убрать кривую АСВ, то наблюдатель будет видеть проекцию А'С'В' кривой, причем углы альфа и бетта составленные проецирующими лучами SA, SC и SC, SB, не изменяются, изображение на сетчатой оболочке глаза также не изменится. Благодаря этому свойству рассматриваемые центральные проекции отличаются большой наглядностью.

Пользуясь чертежом, можно установить некоторые свойства проекций точек. Прямая линия пересекается с плоскостью только в одной точке, поэтому точка имеет на плоскости проекций только одну проекцию, следовательно, точка определяет свою проекцию. Возьмем на одном из проецирующих лучей, например на луче 55, точку D и найдем ее проекцию D'. Она, очевидно, будет совпадать с проекцией В' точки В. Любая точка, взятая на луче SB, будет иметь свою проекцию в той же точке B'D', а это значит, что проекция точки не определяет саму точку, т. е. по одной проекции точки нельзя восстановить положение точки в пространстве.

В связи с тем, что при проецировании кривых линий проецирующие лучи образуют коническую поверхность с вершиной в точке S, центральные проекции иногда называют коническими проекциями, или конической перспективой. Проекция кривой линии рассматривается при этом как линия пересечения проецирующей конической поверхности с плоскостью проекций П'.

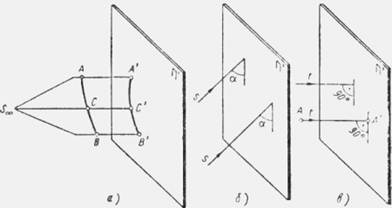
Кроме центрального, существует параллельное проецирование. Если предположить, что центр проекций — точка — удален бесконечно далеко, то проецирующие лучи окажутся практически параллельными друг другу (рис. 2, а); на рисунке показано схематически (как это делалось в геометрии), что проецирующие лучи АА', СС и ВВ' параллельны между собой. Для получения проекций кривой линии АВ на ней берут ряд промежуточных точек и проецируют их с помощью пучка параллельных лучей. Находя точки пересечения этих лучей с плоскостью проекций П', получают проекцию А'С'В' кривой линии АСВ. Как видно, проецирование кривой осуществляется в этом случае с помощью цилиндрической поверхности, в связи с чем параллельное проецирование иногда называют цилиндрическим параллельным проецированием. Различают две разновидности параллельного проецирования: косоугольное и прямоугольное, или ортогональное.

При косоугольном проецировании проецирующие лучи s составляют с плоскостью проекций П' острые углы а (рис. 2, б). При прямоугольном параллельном проецировании проецирующие лучи t составляют с плоскостью проекций П' прямые углы (рис. 2, б). Для того чтобы спроецировать точку А при прямоугольном проецировании, надо опустить перпендикуляр из этой точки на плоскость проекций П' и найти точку пересечения перпендикуляра с плоскостью в точке А'. Отсюда видно, что проекцией точки в прямоугольных проекциях можно называть основание перпендикуляра, опущенного из точки на плоскость проекций.

Прямоугольное проецирование имеет наибольшее распространение в проектной и производственной практике.