
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Микропроцессор как управляющее устройство системы управления. Структура микропроцессорной системой управления приводом постоянного тока.
Рассмотрим некоторые аспекты программирования реальной системы на основе микропроцессорного устройства. Возможный вариант использования микропроцессора (МП) в системе управления двигателем постоянного тока в составе комплектного привода приведен на рис. 1.5.
| МП контроллер |
| АЦП |
| ЦАП |
| комплектный привод |
| Сигнал обратной связи |
| Квантователь с периодом Т |
| цель |
| управления |
Рис. 1.8. Структура процессорной системы управления приводом.
Управляемый привод и микропроцессор связаны через аналого-цифровой (АЦП) и цифроаналоговый (ЦАП) преобразователи. Таким образом, вся система рассматриваться как цифровая система управления с периодом квантования Т секунд.
Пусть целью управления этой системы с двигателем постоянного тока является поддержание скорости нагрузки w(t) постоянной, равной значению задаваемой скорости wd(t). Тогда ошибка между задаваемой скоростью и скоростью нагрузки определяется как
e(t) = wd(t)-w(t) (1.42)
На входе микропроцессора имеется дискретный сигнал ошибки e(k∙T),
k=0,1,2, ..., n. Сигнал на выходе микропроцессора обозначим u(k∙T). Предположим, что микропроцессор должен совершать цифровые вычисления для реализации пропорционально-интегрального (ПИ) регулятора, описываемого в непрерывной форме как
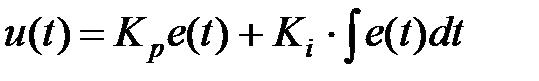 (1.43)
(1.43)
Интеграл в последнем выражении может быть записан в виде
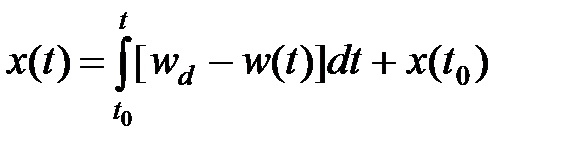 (1.44)
(1.44)
где t0 - начальный момент времени; х(t0) - начальное значение. Для вычисления интеграла могут быть использованы различные методы. Будем использовать метод трапеций и положим t=k∙T, t0=(k-1)·t. Тогда определенный интеграл в выражении (1.44) запишется как
 (1.45)
(1.45)
где t0 – начальный момент времени, x(t0) – начальное значение x(t), k=1,2,…,n. Следовательно, значение интеграла для t=kT может быть вычислено по задаваемой скорости wd и значениям w(kT) и w[(k-1)Т].
Рассчитанное значение управления прикладывается к системе с двигателем постоянного тока при t=(k+1)T, k=0,1,2, … n. Управление изменяется каждые Т секунд и остается постоянным между моментами расчета.
Функциональная схема рассмотренной микропроцессорной системы, используемой для реализации цифрового ПИ-регулятора, приведена на рис. 1.6.
| ЦАП |
| Тиристорный преобразователь |
| Нагрузка |
| МИКРОПРОЦЕССОР |
| ДПТ |
| Тахогенератор |
| АЦП |
| Таймер |
| Шина данных |
| Управляющий код |
Рис. 1.9. Структура функциональных составляющих системы управления.
В этой системе для определения начала следующего периода квантования применен программируемый таймер, который вырабатывает импульс каждый Т секунд. Этот импульс поступает на шину прерываний микропроцессора, что приводит к остановке рабочей программы и выполнению программы прерывания, которая выводит следующее значения управления u[(k + 1)t]. Это управление передается в ЦАП, выходной сигнал которого поступает на вход тиристорного преобразователя. Импульс таймера запускает процесс АЦП-преобразования текущей скорости двигателя w(t) в двоичный код. Для этого процесса требуется конечное время. Следовательно, АЦП должен сообщить микропроцессору через шину готовности о том, что данные преобразованы. После этого процессор вводит значение wd(k·T), и вычисляет следующее значение управления u[(k+1)∙T], которое используется для управления приводом при следующем прерывании от таймера. Аналогично может быть реализован ПИД-регулятор.
Приведенный пример показывает, как управление двигателем постоянного тока может быть реализовано на базе микропроцессора. На начальной стадии решения задачи регулятор описывается дифференциальным уравнением. Последнее записывается с применением одного из приближенных численных методов в дискретной форме для моментов выборки, после чего разрабатывается программа для микропроцессора.
Ограничения микропроцессорных систем управления.
При использовании микропроцессора проектировщик системы должен принимать во внимание конечную длину слова и временные задержки, возникающие при работе программного обеспечения, а так же нелинейность и другие погрешности АЦП преобразования.
В цифровых, микропроцессорных системах управления, вообще говоря, сигналы на входе и выходе являются усеченными. При этом параметры закона управления будут округлены при его реализации в процессоре с помощью рабочей программы. Следовательно, параметры системы могут быть реализованы только конечным набором чисел. На качество микропроцессорных систем управления влияет как конечная длина слова микропроцессора, так и точность выполнения арифметических операций с плавающей точкой.
22. Задачи адаптивного и оптимального управления.
Автоматизация производства, технических объектов и систем представляет собой сложную научно-техническую проблему, которая решается с применением новых технологий, новой техники и методов управления. Большое значение для достижения высоких технико-экономических характеристик технологических объектов имеет теория и методы оптимального и адаптивного управления. Согласно международному стандарту IEEE термин "самоорганизующееся управление" заменил собой термин "адаптивное управление". По этому стандарту процесс управления называется самоорганизующимся, если уменьшение априорных неопределенностей, приводящее к эффективному управления процессом, достигается за счет использования информации, получаемой в ходе процесса управления из последовательных наблюдений доступных входных и выходных сигналов. Самоорганизующийся процесс управления называется параметрически адаптивным, если в процессе управления уменьшается априорная неопределенность некоторого вектора параметров, и функционально адаптивным, если в процессе управления осуществляется непосредственное уменьшение неопределенностей, приводящее к улучшению качества процесса.
Постановка задачи оптимального управления формулируется следующим образом [3]. Пусть поведение модели объекта управления описывается обыкновенным дифференциальным уравнением
 , (1.46)
, (1.46)
где x – вектор состояния системы, x=(xl,...,xn)T  Rn, u – вектор управления, u=(u1,...,uq)T
Rn, u – вектор управления, u=(u1,...,uq)T 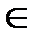 U – некоторое заданное множество допустимых значений управления, t – время, t
U – некоторое заданное множество допустимых значений управления, t – время, t 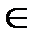 Т=[t0,t1] – интервал времени функционирования системы; вектop-функция f(t,x,u) – непрерывна вместе со своими частными производными.
Т=[t0,t1] – интервал времени функционирования системы; вектop-функция f(t,x,u) – непрерывна вместе со своими частными производными.
Момент начала процесса t0 задан, а момент окончания процесса определяется первым моментом достижения точкой с фазовыми координатами (t,x(t)) некоторой поверхности Г 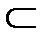 Rn+1 , где Rn – n-мерное евклидово пространство.
Rn+1 , где Rn – n-мерное евклидово пространство.
Т.е. в момент времени t1 должны выполняться условия
Гi(t1,x(t1))=0, i=1,…,k , (1.47)
где 0<k<n+1.
При k=n+1 множество Г представлено точкой в пространстве Rn+1. Начальное условие x(t0)= х0 задает начальное состояние в пространстве Rn+1.
Предполагается, что при управлении используется информация, доступаня в текущий момент времени, т.е. система управления в данном случае является разомкнутой по состоянию и рассматривается так называемое программное управление (рис. 1.10). Множество допустимых управлений U0 образуют кусочно-непрерывные функции u(•). Определим множество допустимых процессов D(t0,x0) как множество троек d=(t1,x(•),u(•)), которые включают момент времени окончания процесса t1, траекторию x(•) и управление u(•), где функции x(•) непрерывны и кусочно-дифференцируемы, а u(•) – кусочно-непрерывны.
| u(t) |
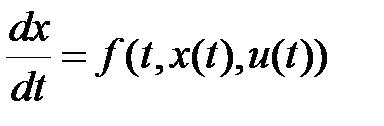
|
| x(t) |
| t |
| X0 |
Рис. 1.10. Программное траекторное управление объектом.
На множестве D(t0,x0) определим функционал качества управления
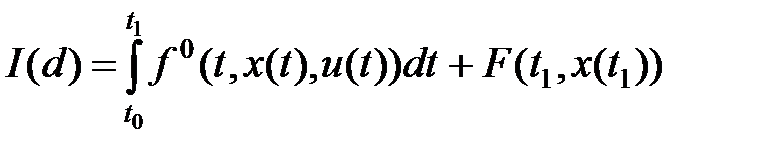 , (1.47)
, (1.47)
где 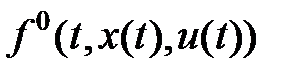 – заданные непрерывно дифференцируемые функции. Требуется найти такую тройку
– заданные непрерывно дифференцируемые функции. Требуется найти такую тройку 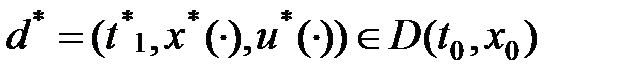 , что
, что
I(d*)=min I(d) (1.48)
Задача (1.48) с функционалом (1.47) называется задачей Больца. Если в функционале отсутствует 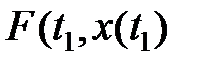 , так называемый терминальный член, то это – задача Лагранжа. Искомые функции x*(•), и u*(•) называются соответственно оптимальной траекторией и оптимальным управлением, а t1* – оптимальным временем окончания процесса.
, так называемый терминальный член, то это – задача Лагранжа. Искомые функции x*(•), и u*(•) называются соответственно оптимальной траекторией и оптимальным управлением, а t1* – оптимальным временем окончания процесса.
Дата добавления: 2015-04-18; просмотров: 386; Мы поможем в написании вашей работы!; Нарушение авторских прав |