Алгоритм решения транспортной задачи линейного программирования методом потенциалов

Алгоритм метода потенциалов, применяемого при решении транс­портной задачи линейного программирования (ТЗЛП), состоит из следующих действий:

1) построение матрицы (таблицы) транспортной задачи. Каж­дая клетка матрицы обозначает транспортную связь между поставщиком и потребителем.

Строки матрицы соответству­ют поставщикам, а столбцы - потребителям. В верхнем углу каждой клетки записывается стоишость перевозки (оценка транспортной связи). Справа от кааждой строки матрицы за­писывается объем производства, а внизу каждого столбца - объем потребления груза. Объемы перевозок будут записы­ваться в клетки матрицы;

2) построение начального (базисного) плана перевозок. Для по­строения базисного плана в ТЗЛП существует несколько мето­дов, наиболее распространенными из которых являются метод «северо-западного угла» и метод наименьшей стоимости. По методу «северо-западного угла» распределение объемов перевозок начинается с верхней левой клетки матрицы. В нее помещается минимальное из двух значений: объем производ­ства первого поставщика; объем спроса первого потребителя. Если объем предложения первого поставщика превышает спрос первого потребителя, то излишки продукции отправля­ются второму потребителю. И наоборот, если объем спроса первого потребителя превосходит возможности первого по­ставщика, то недостающий объем поставляется от второго по­ставщика. Объемы производства остальных поставщиков рас­пределяются аналогичным образом. Метод наименьшей стои­мости отличается от метода «северо-западного угла» тем, что перевозки в нем в первую очередь распределяются по клеткам с наименьшей оценкой. Количество заполненных перевозками клеток должно быть на единицу меньше суммы количества по­ставщиков и потребителей. В противном случае возникает слу­чай вырождения, затрудняющий решение ТЗЛП, поэтому необходимо так перераспределить перевозки в базисном плане, чтобы их количество удовлетворяло указанному условию;

3) построение системы потенциалов по методике, описанной в предыдущем пункте; ( ).

4) расчет разности потенциалов(положительных сдвижек)для клеток, не загруженных перевозками (свободных клеток). Величина положительной сдвижки равна разности между по­тенциалом строки, потенциалом столбца и оценки свободной клетки, находящейся на их пересечении. Если положитель­ные сдвижки (значение которых больше 0) отсутствуют, то оптимальный план перевозок найден;

перераспределение перевозок. Для определения клеток, из которых удаляются перевозки, и клеток, на которые перено­сятся перевозки, в матрице строится замкнутый прямоуголь­ный контур. Первой вершиной контура должна быть незаня­тая клетка с максимальной положительной сдвижкой. Ос­тальные вершины контура должны находиться в занятых клетках. Вершины контура нумеруются (1, 2, 3, ...), начиная с вершины, находящейся в незанятой клетке, либо пооче­редно помечаются знаками + и -, начиная со знака + в неза­нятой клетке. Нумерация или пометка может производиться в любом направлении движения по контуру. Определяется минимальный объем перевозок в четных клетках либо в клетках, помеченных знаком Этот объем перевозок переносится из четных клеток (со знаком -) в нечетные клетки (со знаком +);

5) проверить правильность вычислений. Для этого достаточно сравнить суммарные затраты на перевозку груза по новому плану с затратами базисного (или предыдущего) плана пе­ревозок. Уменьшение затрат является признаком правиль­ности вычислений. Итерации повторяются с пункта 3 до тех пор, пока имеется хотя бы одна положительная сдвижка.

3) Транспортная сеть - это формализованное представление реальных транспортных коммуникаций в виде системы элементов двух типов:вершин (железнодорожных станций, городов, пунктов отправления, назначения) идуг (железных или автомобильных дорог), соединяющих вершины. Вершины обозначаются номерами или индексами i,j. Дуга обозначается номерами вершин, которые она соединяет, например (i,j) или просто ij. Каждая дуга имеет оценку ру, которая определяет длину дуги (расстояние между вершинами) или затраты на движение по дуге. Когда затраты при движении по дуге в одном направлении отличаются от затрат при движении в другом направлении, то оценка дуги записывается в виде дроби. Числитель дроби является оценкой дуги, начинаю- щейся в вершине с меньшим номером, а знаменатель – оценка дуги противоположного направления. Если движение по дуге в ка­ком-либо направлении запрещено, то соответствующая оценка равна М- максимально большому положительному числу.

Маршрут - это последовательность прохождения вершин транс­портной сети при движении от начальной вершины (пункта отправле­ния) до конечной вершины (пункта назначения). Обозначается мар­шрут путем перечисления номеров вершин, то есть S_t . [/,,г₂,...г_и].

Длина (оценка) маршрута - это сумма длин (оценок) дуг, соединяю­щих вершины маршрута.Оптимальный (кратчайший, дешевый) маршрут - это такой маршрут от заданной начальной до конечной вершины маршрута, что не существует другого маршрута с меньшей длиной между этими вершинами.Предшествующая вершина - вер­шина, которая в маршруте предшествует заданной вершине. Обозна­чается ка 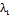,-, где - номер вершины, предшествующей вершине i в маршруте. Для начальной вершины маршрутаа 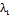=0. Потенциал вершины - это сумма оценок дуг, входящих в маршрут движения от начальной вершины до данной. Обозначается как p_i. Потенциал ко­нечной вершины маршрута равен длине (оценке) всего маршрута.