И использования таблицы оптимальных путей транспортной сети

Таблица оптимальных путей (ТОП) на транспортной сети - это табличное представление всех оптимальных путей от одной или нескольких заданных вершин до всех остальных вершин транс­портной сети. Достоинством ТОП является компактность записи оптимальных путей, которая, в отличие от матричной формы, по­зволяет описать все оптимальные пути, а не только путь между двумя заданными вершинами транспортной сети.

Таблица оптимальных путей состоит из трех столбцов. Первый столбец содержит номера вершин транспортной сети i, второй стол­бец - номера предшествующих вершин 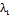,-, третий - потенциалы вершин pi. Кратчайший маршрут до i-й вершины определяется по номерам предшествующих вершин. Для г'-й вершины по таблице на­ходится предшествующая, для нее - своя предшествующая вершина и т.д., до тех пор, пока не будет определена начальная вершина маршрута, для которой не задана предшествующая вершина. Потенциал каждой вершины равен расстоянию от начальной вершины до данной вершины при движении по оптимальному маршруту.

Алгоритмпостроения ТОП состоит из следующих действий:

1) заполнить первый и второй столбцы ТОП номерами вершин транспортной сети в порядке их возрастания. Во втором столбце одну или несколько начальных вершин пометить, на­пример, знаком минус перед номерами вершины. Третий стол­бец заполнить исходными потенциалами вершин. Исходные потенциалы начальных вершин равны нулю, а всех остальных вершин - числу М или максимально большому числу;

2) для всех дуг, исходящих из помеченной вершины, проверя­ется условие оптимальности дуги p. — p_t > p_iJt то есть раз­ность потенциалов конечной и начальной вершин дуги долж­на быть больше оценки дуги между этими вершинами. Вы­полнение этого условия говорит о выгодности движения по данной дуге. Тогда в качестве предшествующей вершины для конечной вершины дуги (второй столбец ТОП) указыва­ется номер вершины i (с пометкой). Потенциал конечной вершины определяется как сумма потенциала начальной вершины дуги и оценки этой дуги, то есть pj — р. + p_tj;

3) если условие оптимальности дуги не выполняется, то прове­ряется следующая дуга, исходящая из помеченной вершины;

4) если условие оптимальности проверено для всех дуг, исхо­дящих из помеченной вершины, то метка с этой вершины снимается, и рассматриваются дуги, исходящие из любой следующей помеченной вершины. Затем все действия, на­чиная со второго, повторяются. Построения оптимальных маршрутов повторяются до тех пор, пока в ТОП имеется хо­тя бы одна помеченная вершина.

В процессе построения ТОП возможна многократная корректи­ровка потенциалов вершин и номеров предшествующих вершин, по­этому принято строить несколько таблиц с переносом в новую таб­лицу результатов предыдущих построений.