Сетевые модели. Детерминированные модели.

Общая характеристика

Информация, содержащаяся в ПДВ — наименее сложной и Наиболее широко применяемой в системах СПУ, состоит из описания детерминированной сети с единственным исходным событием iω и единственным завершающим событием ia, а также следующих временных характеристик: детерминированные продолжительности t_ij всех работ ij (фиктивным работам приписывается нулевая продолжительность) и момент Т0 начала выполнения комплекса работ. Если этот момент не задан, то условно принимают Т0=0. Может быть также задан директивный срок Тдир наступления завершающего события iω.

Несмотря на упрощенность такой модели, ее использование позволяет эффективно решать ряд задач организации и управления строительством.

Б. Правила построения сетевой модели комплекса

Для построения сетевой модели типа «работы — дуги» необходимо каждую работу, реально выполняемую на стройке, представить как дугу (стрелку) с таким расчетом, чтобы различным работам отвечали различные дуги и чтобы между этими дугами сохранились те же взаимосвязи (отношения предшествования), которые имеют место для соответствующих работ в практике строительства. Так, если монтаж фундаментов предшествует их обратной засыпке, то и дуга, обозначающая закладку фундаментов, должна предшествовать дуге, отображающей обратную засылку.
При построении сетевой модели типа «работы — вершины» каждая реальная работа соответствует определенной вершине, которой и присваивают название этой работы. Дуги (стрелки), соединяющие вершины, являются связями и обозначают условие предшествования между работами (рис. 1).

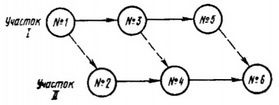
Рис. 1. Сеть типа «работы — вершины»: № 1, 2 — отрывка котлована на участках I и II: № 3,4 — то же, монтаж фундаментов; № 5,6 — то же, обратная засыпка; сплошные стрелки — технологические связи; штриховые — ресурсные связи, обусловленные переходами машин, бригад рабочих с одной работы на другую

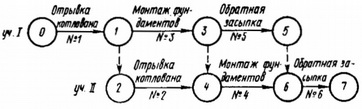
Рис. 2. Сеть типа «работы — дуги»: цифры в кружках — номера событий; штриховые стрелки — фиктивные работы

На рис. 2 показана модель типа «работы — дуги», соответствующая сетевой модели «работы — вершины», приведенной на рис. 1. Здесь каждая работа имеет лишь одной ей присущее сочетание начального и конечного событий. Поскольку наибольшее распространение получили сетевые модели «работы — дуги», рассмотрим подробнее правила их построения:

стрелки, обозначающие работы, рекомендуется (хотя это не строго обязательно) изображать горизонтальными линиями и направлять слева направо, по возможности избегая пересечений; стрелки (работы) должны быть связаны между собой так, чтобы оказались зафиксированными все действительные зависимости. Вместе с тем нельзя допускать включения в сетевую модель искусственных, надуманных зависимостей, искажающих истинное положение вещей и существенно снижающих возможности оптимизации и реального использования сетевой модели. Так, в примере, приведенном на рис. 1, работы 2 и б непосредственно предшествуют работам 4 и 5. Однако изображать при построении сетевой модели типа «работы — дуги» эти работы и связи так, как показано на рис. 3, а я б, нельзя. Получилось бы, что в случае а начало монтажа фундаментов на участке II (работа 4) вообще не зависит от окончания монтажа на участке I (работа 3), что неверно, а в случае б — что приступить к обратной засыпке на участке I (работа 5) невозможно без отрывки котлована на участке II (работа 2), что также неправильно.

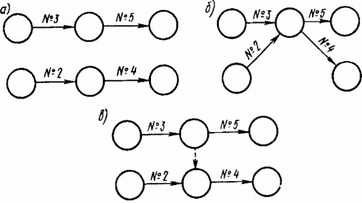
Рис. 3. Изображение зависимости между работами № 2 и 3 и № 4 и 5: а и б — неправильное; в — правильное событие

Для правильного отражения ситуации следует ввести фиктивную работу (связь) и дополнительное событие, как показано на рис. 3, в. Указанное решение приведено и на рис. 2, где показаны работы 2—4 и 3—5, соответствующие работам 2 и 5 на рис. 1 и 3 и работы 1—3 и 4—6, соответствующие работам 3 и 4 на рис. 1 и 3.

Рис. 4. Изображение параллельно выполняемых работ: а — неправильное; б — правильное

Нельзя допускать, чтобы две или более работы имели одинаковую комбинацию начального и конечного событий. Поэтому неправилен пример, приведенный на рис. 4, а. Следует ввести фиктивные работы и дополнительные события (рис. 4, б), обеспечивающие для каждой работы лишь ей присущее сочетание начального и конечного событий;

если какие-либо работы b, c, d, e могут быть начаты после частичного окончания работы А, то последнюю нужно разбить на части, соответственно предшествующие началу производства работ b, c, d, и е. Каждая выделенная часть работы А — а1, а2 и т. д. рассматривается в этом случае как отдельная работа (рис. 5);

если для начала работы с надо завершить работу а и работу Ь, в то время как для того, чтобы приступить к работе d достаточно закончить только работу а, а фронт работы е открывает лишь работа Ь, то следует ввести дополнительное событие и фиктивные связи (рис. 6.);

в сети не должно быть циклов и тупиков. Наличие цикла (замкнутого контура), характеризующегося тем, что цепочка работ возвращается к тому же событию, из которого вышла, свидетельствует об искажении отношений порядка между работами, так как каждая работа цикла оказывается предшествующей самой себе, что лишено смысла (рис. 7, циклы 2—6—7—8—2 и 2—3—5—8—2).

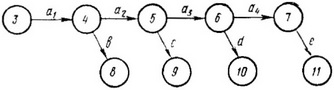
Рис. 5. Разбивка работы на части для открытия фронта работ другим работам

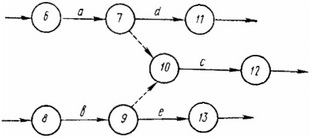
Рис. 6. Сложный случай зависимостей между пятью работами

Рис. 7. Примеры циклов и тупиков в сети: циклы: 1) 2—3—5—8—2—2) 2—6—7—8—2; тупики: 4 и 9

Тупик — это любое событие (кроме завершающего), из которого не выходит ни одна работа, либо какое-либо событие (кроме исходного), в которое не входит ни одна работа (рис. 11 соответственно события 9 и 4).

Детальные сетевые модели при необходимости могут укрупняться, при этом группа работ на детальной модели заменяется одной работой на укрупненной. Однако такое укрупнение возможно лишь в случае, если вся заменяемая группа работ имеет одно начальное и одно конечное события. Длительность введенной в модель укрупненной работы равна длительности наибольшего пути (цепочки работ) от начального до конечного события заменяемой группы работ, (рис. 12,6). Так, на рис. 6.12, а наибольший путь 6—8—9—12 равен 17 дням. Важно и то, чтобы все работы группы выполнялись силами одной организации.

Рис. 8. Примеры укрупнения фрагментов сетевого графика: а — простейший случай с одной входной и выходной работой (до укрупнения); б — то же, после укрупнения; в — сложный случай при более чем по одному событию с входными и выходными работами (до укрупнения); г — то же, после укрупнения

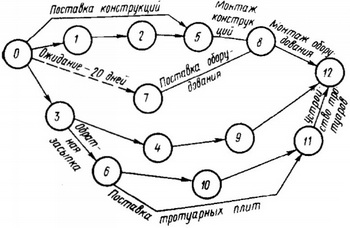
Рис. 9. Изображение «внешней» работы на сетевом графике: случай отсутствия ограничений на срок начала «внешней» работы 0—5; случай зависимости такого начала с окончанием какой-либо работы сети («внешняя» работа 6—11); случай указания дня, не ранее которого может быть начата «внешняя» работа 7—8

На рис. 8,6 показан более сложный случай, когда группа работ имеет более чем одно входное и одно выходное события. В этом случае, как следует из рис. 8, г, удается укрупнить лишь отдельные участки, каждый из которых в свою очередь имеет одно начальное и одно конечное событие;

в сетевую модель могут быть введены не только строительно-монтажные, но и так называемые «внешние» работы — поставки конструкций, оборудования и др. Любая такая «внешняя» работа должна входить в начальное событие той строительно-монтажной работы, которая обеспечивается соответствующей поставкой (рис. 9). Начало «внешней» работы вводится в исходное событие всей сетевой модели, если не оговорены особые условия начала поставки (работа 0—5 на рис. 9). Примером особых условий может быть ограничение возможности начала складирования лишь после обратной засыпки фундаментов (работа 6—11) или начала завоза соответствующих конструкций не ранее определенного дня (работа 7—8). В первом случае начальное событие «внешней» работы связывается с конечным событием обратной засыпки (событие 6), во втором — вводится фиктивная работа — «ожидание» (1—7) между исходным событием сетевой модели и начальным событием «внешней» работы;

в сетевой модели, отражающей увязку строительных процессов на захватке, не следует допускать неверных (в действительности не существующих) зависимостей между процессами, выполняемыми на разных захватках. Так, на рис. 6.14, а неправомерно оказались во взаимозависимости обратная засыпка на 1-й захватке (работа 3—5) и отрывка котлована на 2-й захватке (работа 1—2) из-за связи 2—3. Точно так же не должен монтаж колонн на 1-й захватке (работа 5—7) зависеть от монтажа фундамента на 2-й захватке (работа 3—4) и отрывки котлована на 1-й захватке (работа 2—4), а связь 4—5 неправомерно фиксирует такую зависимость. Чтобы избежать перечисленных и других неверных связей, надо ввести фиктивные работы и дополнительные события, что и 1 сделано на рис. 10, б.

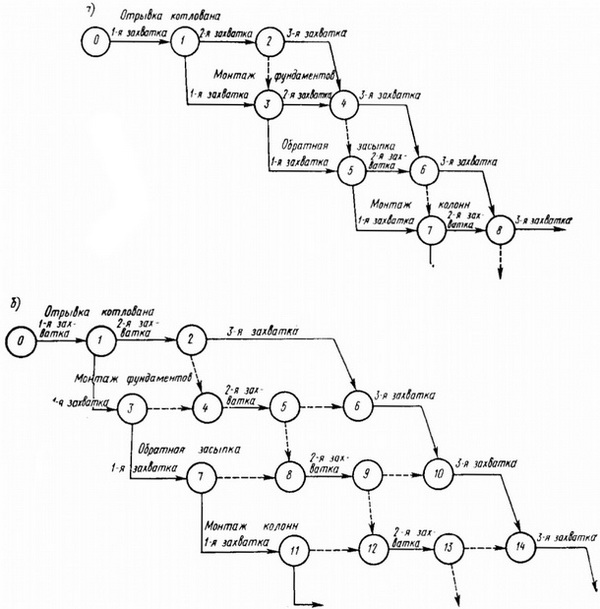
Рис. 10. Изображение увязки строительных процессов на захватке: а — неправильно; б — правильно

28. Системы сетевого планирования и управления. Организационная структура системы.

Прообразом программы в программно-целевом методе планирования инноваций часто выступает сетевой график. Последний составляется для выполнения программы, он отражает все ра­боты, необходимые для достижения цели.

Сетевой график – это модель достижения поставленной цели, причем цель является моделью, динамично приспособленной для анализа вариантов достижения цели, для оптимизации плано­вых заданий, для внесения изменений и т.п.

Метод работы с сетевыми графиками – сетевое планирование – базируется на теории гра­фов. В переводе с греческого граф (grafpho – пишу) представляет систему точек, некоторые из них соединены линиями – дугами (или ребрами). Это топологическая (математическая) модель взаимодействующих систем. С помощью графов можно решать не только задачи сете­вого планирования, но и другие задачи. Метод сетевого планирования применяется при планировании проведения комплекса взаимосвязанных работ. Он позволяет наглядно представить организационно-техно­логическую последовательность выполнения работ и уста­новить взаимосвязь между ними. Кроме этого, он позволяет обеспечить координацию операций различ­ной степени сложности и выявить операции, от которых зависит продолжительность всей работы (т.е. организационного меро­приятия), а также сосредоточить внимание на своевременном выполне­нии каждой операции.

Сетевой метод – это система приемов и способов, позволяющих на основе применения сетевого графика (сетевой модели) рациональ­но осуществлять весь управленческий процесс, планировать, организовывать, координировать и контролировать любой комп­лекс работ, обеспечивая эффективное использование денежных и материаль­ных ресурсов. Применение этого метода позво­ляет улучшить:

1) планирование, обеспечивая его комплексность, непрерыв­ность, создавая условия для улучшения определения требуемых ресурсов и распределения уже имеющихся ресурсов;

2) финансирование работ, т.к. появляются способы более точ­ного расчет себестоимости работ, их трудоемкости и формиро­вания нормативно-справочной базы;

3) структуру системы управления путем четкого определения и распределения задач, прав, обязанностей;

4) организацию процедур координации и контроля за ходом ра­бот на базе оперативной и точной информации, а также оценку выпол­нения плана.

Сетевой график – это информационная модель, отображающая процесс выполнения комплекса работ, направленных на достижение единой цели. Цель сетевого планирование – воздействие на управ­ление, а управление призвано поддерживать рациональ­ный режим работы, восстанавливать нарушенное состояние под­вижного равновесия динамических систем, обеспечивая слаженную работу всех ее звеньев. При этом управление системой ведется по ряду параметрам: времени, стоимости, ресурсам, технико-экономическим показателям. Однако наиболее распространенными являются системы с параметром «время».

Процесс управления при представлении управляемой системы в виде модели существенно упрощается. Основой сетевого планирования и управления является сетевой график, отражающий тех­нологическую и логическую взаимосвязь всех операций предстоящей работы. Он состоит из трех со­ставных частей (главных понятий), таких как «работа», «событие» и «путь».

«Работа» – это любой процесс, требующий затрат времени и ре­сурсов или только времени. Если на выполнение работы не требуется ресурсов, а зат­рачивается лишь время, то они называются «ожиданием». Работу на сетевом графике обозначают сплошной стрелкой (ду­гой графа), над которой числом обозначается продолжитель­ность выполнения данной работы. Существует фиктивная работа (ожидание, простая зависимость) – работа, не требующая затрат времени, труда и средств. На графике она отоб­ражается пунктирной стрелкой.

Работы в виде стрелки (тогда граф называется ориентированным, или орграфом) на графике не являются векторами, поэто­му вычерчиваются без масштаба. Каждая работа начинается и кончается «событием», которое обо­значается кружочком, в котором цифра обозначает название (имя) данного события. Событие – это результат выполнения одной или нескольких работ, являющийся необходимым для начала после­дующих работ. Предшествующее событие является отправной точ­кой для работы (причиной), а последующее событие – ее результатом.

События в отличие от работ совершаются в определенные момен­ты времени, не используя при этом никаких ресурсов. Начало вы­полнения комплекса работ есть начальное событие. Момент завер­шения всех работ есть конечное событие.

Любой сетевой график имеет одно исходное (начальное) и одно завершающее (конечное) событие. Любая работа – стрелка – соеди­няет только два события.

Событие, из которого стрелка выходит, называется предшествую­щим данной работе, а событие, в которое стрелка входит, является – последующим. Одно и то же собы­тие, кроме исходного и завершающего, является по отношению к од­ной работе предшествующим, а к другой – последующим. Такое со­бытие называется промежуточным. События могут быть простыми и сложными. Простые события имеют только одну входящую и одну выходящую работу.

Сложные события имеют несколько входящих или несколько вы­ходящих работ. Деление событий на простые и сложные имеет большое значение при расчете сетевых графиков. Событие считает­ся свершившимся, когда будет закончена самая длинная по продолжительности из всех входящих в него работ.

Непрерывная технологическая последователь­ность работ (цепь) от первого события до последнего называется путем. Такой путь является полным путем. Полных путей может быть несколько. Длина пути определяется суммой продолжительности лежащих па нем работ. Используя метод графиков, можно определить каждый из путей. Это достигается последовательным выявлением элементов каждого пути.

В результате сравнения различных путей выбирают путь, на ко­тором продолжительность всех содержащихся работ наибольшая. Этот путь носит название «критический путь». Он определяет время, необходимое для выполне­ния всего плана, на который составлен график. Именно от работ, лежащих на критическом пути, и их продолжи­тельности зависит конечный срок выполнения плана.

Критический путь – основа оптимизации плана. Для того чтобы сократить срок выполнения всего плана, необходимо уменьшить продолжительность выполнения тех работ, которые на­ходятся на критическом пути.

Все полные пути, продолжительность которых меньше критиче­ского, называются некритическими. Они обладают резервами вре­мени. Под резервами времени понимаются допустимые сдвиги сро­ков совершения событий и выполнения работ, не меняющие сроков наступления завершающего события.

Резервы времени бывают полные и свободные. Полный резерв времени – это срок, на который можно перенести начало работы или увеличить ее продолжительность при неизмен­ной длине критического пути. Полный резерв времени определяют как разность между поздним и ранним началом работы или между поздним и ранним окончанием работы.

Работы критического пути полного резерва времени не имеют, т.к. их ранние параметры равны поздним. Использование полного ре­зерва времени на других некритических путях приводит к тому, что путь, к которому принадлежал запас времени, становится критическим.

Свободным резервом времени называется срок, на который мож­но перенести начало работы или увеличить ее продолжительность при условии, что ранние начала последующих работ не изменяются. Этот резерв времени используют в том случае, когда в одно событие входит две и более работ. Свободный резерв времени определяют как разность раннего начала последующей работы и раннего окон­чания рассматриваемой работы.

Резерв времени позволяет увеличить продолжительность выпол­нения работ или же начать их несколько позднее, а также дает воз­можность маневрировать внутренними финансовыми, материаль­ными и трудовыми ресурсами (деньгами, количеством техники, численностью работников, временем начала работ).

Анализируя сетевые графики, можно заметить, что они отлича­ются не только количеством событий, но и числом взаимосвязей между ними. Сложность сетевого графика оценивается коэффициентом слож­ности. Коэффициент сложности представляет собой отношение количества работ сетевого графика к количеству событий и определя­ется по формуле:

К = Р / С ,

где К – коэффициент сложности сетевого графика;

Р и С – количество работ и событий, ед.

Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.

Приступая к построению сетевого графика, следует установить:

1) какие работы должны быть завершены ранее, чем начнется дан­ная работа;

2) какие работы могут быть начаты после завершения данной ра­боты;

3) какие работы могут выполняться одновременно с данной работой. Кроме того, надо придерживаться общих положений и правил:

а) сеть вычерчивается слева направо (это же направление имеют и стрелки-работы);

б) каждое событие с большим порядковым номером изображается правее предыдущего;

в) график должен быть простым, без лишних пересечений;

г) все события, кроме завершающего, должны иметь последую­щую работу (в сети не должно быть события, кроме исходного, в которое не входила бы ни одна работа);

д) один и тот же номер события нельзя использовать дважды;

е) в сетевом графике ни один путь не должен проходить дважды через одно и то же событие (если такие пути обнаружены, то это свидетельствует об ошибке);

ж) если начало какой-либо работы зависит от окончания двух предшествующих работ, выходящих из одного события, тогда между событиями – окончаниями этих двух работ – вводится фиктивная работа (зависимость).

Использование сетевых моделей способно оказать существенную помощь в планировании и осуществлении мероприятий в рамках инновационного менеджмента, поэтому ими нельзя пренебрегать.

Системы сетевого планирования и управления. Функциональная структура системы.

Общепринятые методики управления проектами, стандарты и ключевые термины содержатся в Руководстве по управлению проектами "Project Management Body of Knowledge" (PMBOK), которое, по существу, является сводом профессиональных знаний по управлению проектами. Само понятие "проект" широко используется в повседневной жизни. В теории управления проектами этот термин является ключевым, и в руководстве PMBOK приведено следующее определение: "проект - это временное предприятие, предназначенное для создания уникальных продуктов, услуг или результатов.

При этом, "термин "временное" означает, что у любого проекта есть четкое начало и четкое завершение. Завершение наступает, когда достигнуты цели проекта; или осознано, что цели проекта не будут или не могут быть достигнуты; или исчезла необходимость в проекте, и он прекращается"

Проекты могут различаться своими целями, масштабом, протяженностью во времени, сферой деятельности и т.д. Но у всех проектов обязательно определена конкретная цель, и она является уникальной; выделены ресурсы и существуют временные рамки для достижения цели.

Отличие проекта от повседневной операционной деятельности состоит в наличии у проекта уникальной цели и временных ограничений. Повседневные операции выполняются постоянно, имеют повторяющийся характер, в то время как " проекты являются временными и уникальными".

"Конечные цели проекта и операционной деятельности отличаются коренным образом. Задача проекта - достижение поставленной цели, после чего проект завершается. Операционная деятельность, напротив, обычно служит для обеспечения нормального течения бизнеса. Проект отличается тем, что он завершается после выполнения поставленных конкретных задач, в то время как операции получают новые цели и продолжают выполняться".

"Проекты являются средством организации операций, которые не могут быть проведены в рамках обычной деятельности организации. Таким образом, проекты часто используются в качестве средства выполнения стратегического плана организации".

Под управлением проектом понимается деятельность, направленная на эффективное достижение целей проекта в установленные строки, в рамках утвержденного бюджета, с заданным качеством.

"Управление проектами - это приложение знаний, навыков, инструментов и методов к операциям проекта для удовлетворения требований, предъявляемых к проекту. Управление проектами выполняется с помощью применения и интеграции процессов управления проектами: инициации, планирования, исполнения, мониторинга и управления, завершения."

"В управление проектом входит):

· Определение требований

· Установка четких и достижимых целей

· Уравновешивание противоречащих требований по качеству, содержанию времени и стоимости

· Коррекция характеристик, планов и подхода в соответствии с мнением и ожиданиями различных участников проекта".

Итак, управление проектом состоит в планировании, организации и управлении задачами и ресурсами для достижения цели проекта и контроле стратегии реализации проекта.

Управление проектами - это область менеджмента, охватывающая те сферы производственной деятельности, в которых создание продукта или услуги реализуется как уникальный комплекс взаимосвязанных целенаправленных мероприятий при определенных требованиях к срокам, бюджету и характеристикам ожидаемого результата.

В качестве субъектов управления в системе управления проектами (СУП) рассматриваются активные участники проекта, взаимодействующие при выработке и принятии управленческих решений. К ним относятся:

· управленческий аппарат заказчика проекта, включая все необходимые подразделения и организации, представляющие различные роли заказчика (например, инвестор, функциональный заказчик, генеральный заказчик и др.);

· управленческий аппарат исполнителя (или исполнителей) проекта, включая все необходимые подразделения и организации, представляющие различные роли исполнителя (например, генеральный подрядчик, генеральный системный интегратор, подрядчик, субподрядчик, поставщик и др.);

· команды проектов (группы управления, рабочие группы) - специализированные организационные структуры, создаваемые на время выполнения проектов и включающие управленческий и технический персонал, выделяемый заказчиком и исполнителями для выполнения проектов.

В качестве объекта управления рассматриваются:

· портфель проектов - совокупность проектов, находящихся в компетенции одного центра ответственности;

· программа - группа взаимосвязанных проектов и различных мероприятий, объединенных общей целью и условиями их выполнения. Управление проектами, объединенными в рамках одной программы, обычно требует координации. Программы обычно включают в себя элемент непрерывной деятельности;

· проект - комплекс взаимосвязанных мероприятий, предназначенных для достижения поставленных целей с установленными требованиями к качеству результата в течение заданного времени и при установленном бюджете;

·

· стадии жизненного цикла программ и проектов - набор логически взаимосвязанных работ проекта, в процессе завершения которых достигается один из основных результатов проекта. Жизненные циклы проектов в различных областях деятельности могут существенно различаться.

Процессы управления проектом осуществляются на всех стадиях жизненного цикла проекта и могут быть классифицированы по двум следующим основаниям - по области применения (области знаний) и по целевому результату (фазы управления).

К областям знаний в проекте относится управление содержанием и границами проекта, управление проектом по временным и стоимостным параметрам, управление качеством, отклонениями и др.

Под фазой процесса управления понимается совокупность мероприятий (процессов), обеспечивающих достижение одного из следующих результатов:

· санкционирование начала проекта или очередной стадии его жизненного цикла - инициализация;

· определение наилучшего способа действий для достижения целей стадии жизненного цикла проекта с учетом складывающейся обстановки - планирование;

· реализация плана стадии жизненного цикла проекта (от выдачи задания до получения результата) - выполнение;

· выявление фактов отклонения фактического выполнения стадии жизненного цикла проекта от запланированного и принятие корректирующих действий - контроль;

· завершение и закрытие проекта или стадии жизненного цикла проекта - завершение.

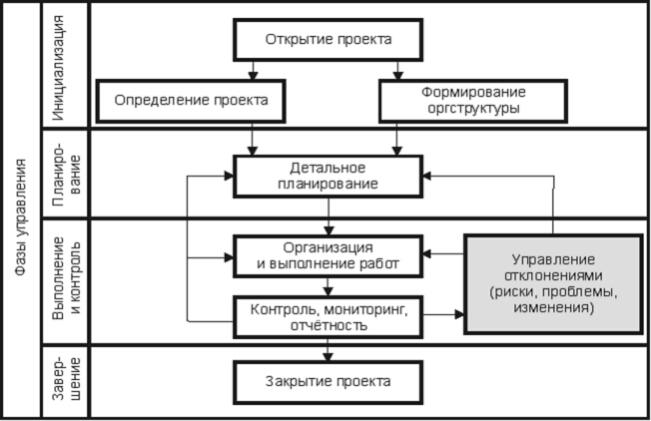
Рисунок 1 - Процессы управления проектами

Оперативное управление в системах сетевого планирования и управления.

Разработка методических основ формирования оптимальных календарных планов-графиков предполагает выбор математической модели, полностью отражающей производственный процесс на предприятии. В частности, при этом важно учитывать порядок выполнения операций. Построение в этом случае адекватной модели невозможно без сетевого графика.

Использования системы сетевого планирования и управления (СПУ) в качестве математической модели сложного производственного процесса изготовления продукции ведет к переводу экономических расчетов на строгие математические основы. Сеть обеспечивает возможность осуществления взаимоувязки и координации движения всего множества заказов, находящихся в производстве. При этом отдельные заказы (их маршруты) выступают как элементы единой системы, которая может быть подвергнута всестороннему анализу. Сетевой график наглядно отражает существующие между операциями производственного процесса взаимосвязи, позволяет довольно точно определять обязанности между исполнителями.

Сетевая модель трактуется как модель комплекса работ, обязательной составляющей которой является сеть комплекса. Сеть комплекса рассматривается как абстрактное понятие, как ориентированный граф, отображающий отношения предшествования и непосредственного предшествования между работами комплекса. Допускается существование двух равноправных типов сетей, в одном из которых работам комплекса сопоставлены дуги (ветви) графа, а в другом - вершины графа. В отечественной литературе наибольшее распространение получили сетевые модели типа работы-дуги.

Несмотря на их широкую применимость, сетевые модели типа работы-дуги обладают одним очень существенным недостатком. При осуществлении параллельного или параллельно-последовательного вида движения предметов труда по операциям производственного процесса сети типа работы-дуги требуют введения большого количества фиктивных операций. А это значительно усложняет сеть, увеличивает объем требуемой информации при подготовке данных для расчета параметров сети.

Производственный процесс изготовления сложной продукции на предприятии может быть представлен сетевым графом без петель и контуров. Таким образом, выполняется основное требование, предъявляемое к моделируемому процессу в системе СПУ.

Особенность задач календарного планирования заключается в наличии множественности возможных вариантов решений и, следовательно, возможности выбора наилучшего из них.

Возможны два варианта постановки задачи оптимизации. Первая из них предусматривает достижение максимального конечного результата при заданных ресурсах, а вторая - заданного конечного результата при минимальных затратах производственных ресурсов. Задача построения оптимальных планов-графиков рациональной организации производства может быть сведена к первому варианту.

Последовательность решения задачи оптимального управления производством включает в себя постановку задачи; определение цели; выбор критерия оптимальности; математическую формулировку задачи; выбор эффективного экономико-математического метода; разработку алгоритма программы и расчет.

В ходе оперативного управления производством на предприятиях решаются два типа оптимизационных задач. В задачах первого типа определяется оптимальный порядок запуска изделий в производство с целью получения минимальной длительности производственного цикла отдельных изделий. В ходе рассмотрения такой задачи решается проблема оптимальной организации производственного процесса во времени. Для решения этого типа задач используются модели объемно-календарного планирования, а в качестве оптимизационного метода - один из методов теории расписаний.

Задачи второго типа заключаются в оптимизации использования производственных ресурсов предприятия с целью достижения рациональной организации производственного процесса в пространстве. Такие задачи решаются с использованием модели объемного планирования и методов линейного программирования.

В традиционной постановке задачи календарного планирования минимизируется один из следующих критериев оптимальности:

- общее время обработки всех деталей (длительность совокупного производственного цикла);

- суммарное пролеживание деталей;

- суммарный простой станков;

- суммарное отклонение от плановых сроков окончания обработки заказов;

- средняя длительность пребывания заказа в обработке.

Критерием оптимальности, наиболее полно отражающим требование наилучшего использования производственных ресурсов (при обеспечении минимальных сроков выпуска изделий), основного требования, предъявляемого при решении задач календарного планирования, является минимум длительности совокупного производственного цикла изготовления месячного портфеля заказов.

Чем меньше значение этого показателя, тем плотнее составлено расписание, а значит, лучше используются производственные мощности предприятия, его материальные и трудовые ресурсы.

В свою очередь, длительность совокупного производственного цикла в значительной мере зависит от очередности обработки заказов на отдельных операциях производственного процесса.

Условие обеспечения минимальной длительности производственного цикла отдельных изделий приводит к необходимости решения так называемой «задачи упорядочения» с сохранением очередности обработки заказов на всех операциях производственного процесса постоянной. В этом случае процесс оптимизации заключается в выборе такого порядка запуска изделий в производство, который обеспечил бы минимально возможную длительность совокупного производственного цикла и минимум простоев оборудования.

Модель оптимизации графиков движения изделий в производстве с минимальной длиной расписания в сетевой постановке должна включать целевую функцию, отображающую условия наиболее эффективного выполнения комплекса работ; систему топологических ограничений, вытекающих из структуры графа; систему ограничений на используемые ресурсы .

Зная правила приоритетности запуска изделий в производство и используя в качестве модели производственного процесса на предприятии систему сетевого планирования и управления (СПУ), можно обоснованно осуществлять все календарно-плановые расчеты производства:

- рассчитать сквозной попроцессный (на межцеховом уровне) и пооперационный (на внутрицеховом уровне) графики прохождения конкретного заказа в производстве;

- увязать их сроки с прохождением других заказов;

- провести расчеты по выбору наилучшего варианта плана с позиции минимальной длительности цикла и максимальной загрузки оборудования;

- рассчитать календарный график загрузки оборудования и рабочих мест;

- получить график выпуска полуфабрикатов.

То есть применение системы СПУ и знание правила приоритетности запуска решений в производство позволяет рационально спланировать и скоординировать работу цехов и участков предприятия во времени и пространстве. Выходными документами процесса оперативно-календарного планирования в этом случае будут оперативный план предприятия на месяц, пооперационные графики прохождения изделий в производстве, графики выпуска полуфабрикатов и готовой продукции, графики загрузки оборудования и поточных линий, а также графики плотности работ наборных участков.

31. Сетевая модель – модель календарного управления.

Сетевой график основан на использовании другой математической модели - графа. Графам (устаревшие синонимы: сеть, лабиринт, карта и т.д.) математики называют "множество вершин и набор упорядоченных или неупорядоченных пар вершин". Говоря более привычным для инженера (но менее точным) языком, граф - это набор кружков (прямоугольников, треугольников и проч.), соединенных направленными или ненаправленными отрезками. В этом случае сами кружки (или другие используемые фигуры) по терминологии теории графов будут называться "вершинами", а соединяющие их ненаправленные отрезки - "ребрами", направленные (стрелки) - "дугами". Если все отрезки являются направленными, граф называется ориентированным, если ненаправленными - неориентированным.

Наиболее распространенный тип сетевого графика работ представляет систему кружков и соединяющих их направленных отрезков (стрелок), где стрелки отображают сами работы, а кружки на их концах ("события") - начало или окончание этих работ.

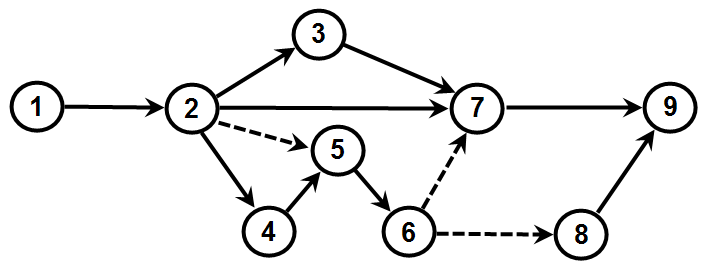
Рисунок показывает упрощенно лишь одну из возможных конфигураций сетевого графика, без данных, характеризующих сами планируемые работы. Фактически на сетевом графике приводится множество сведений о производимых работах. Над каждой стрелкой пишется наименование работы, под стрелкой - продолжительность, этой работы (обычно в днях).

В самих кружках (разделенных на секторы) также содержится информация, смысл которой будет пояснен в дальнейшем. Фрагмент возможного сетевого графика с такими данными представлен на рисунке ниже.

В графике могут использоваться пунктирные стрелки - это так называемые "зависимости" (фиктивные работы), не требующие ни времени, ни ресурсов.

Они указывают на то, что "событие", на которое направлена пунктирная стрелка, может происходить только после свершения события, из которого исходит эта стрелка.

В сетевом графике не должно быть тупиковых участков, каждое событие должно соединяться сплошной или пунктирной стрелкой (или стрелками) с каким-либо предшествующим (одним или несколькими) я последующим (одним или несколькими) событиями.

Нумерация событий производится примерно в той последовательности, в какой они будут происходить. Начальное событие располагается обычно с левой стороны графика, конечное — с правой.

Последовательность стрелок, в которой начало каждой последующей стрелки совпадает с концом предыдущей, называется путем. Путь обозначается в виде последовательности номеров событий.

В сетевом графике между начальным и конечным событиями может быть несколько путей. Путь, имеющий наибольшую продолжительность, называется критическим. Критический путь определяет общую продолжительность работ. Все остальные пути имеют меньшую продолжительность, и поэтому в них выполняемое работы имеют резервы времени.

Критический путь обозначается на сетевом графике утолщенными или двойными линиями (стрелками).

Особое значение при составлении сетевого графика имеют два понятия:

Раннее начало работы - срок, раньше которого нельзя начать данную работу, не нарушив принятой технологической последовательности. Он определяется наиболее долгим путем от исходного события до начала данной работы

Позднее окончание работы - самый поздний срок окончания работы, при котором не увеличивается общая продолжительность работ. Он определяется самым коротким путем от данного события до завершения всех работ.

При оценке резервов времени удобно использовать еще два вспомогательных понятия:

Раннее окончание - срок, раньше которого нельзя закончить данную работу. Он равен раннему началу плюс продолжительность данной работы

Позднее начало - срок, позже которого нельзя начинать данную работу, не увеличив общую продолжительность строительства. Он равен позднему окончанию минус продолжительность данной работы.

Если событие является окончанием лишь одной работы (т.е. в него направлена только одна стрелка), то раннее окончание этой работы совпадает с ранним началом последующей.

Общий (полный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не увеличивая общую продолжительность работ. Он определяется разностью между поздним и ранним началом (или поздним и ранним окончанием - что то же самое).

Частный (свободный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не меняя раннего начала последующей. Этот резерв возможен только тогда, когда в событие входят две или более работы (зависимости), т.е. на него направлены две или более стрелки (сплошные или пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать с ранним началом последующей работы, для остальных же это будут разные значения. Эта разница у каждой работы и будет ее частным резервом.

Кроме описанного типа сетевых графиков, в котором вершины графа ("кружки") отображают события, а стрелки - работы, существует другой тип, в котором вершинами являются работы. Различие между этими типами непринципиальное - все основные понятия (раннее начало, позднее окончание, общие и частные резервы, критический путь и т.д.) сохраняются неизменными, отличаются лишь способы их записи.

Построение сетевого графика этого типа основано на том, что раннее начало последующей работы равно раннему окончанию предыдущей. Если данной работе предшествует несколько работ, ее раннее качало должно быть равно максимальному раннему окончанию предыдущих работ. Расчет поздних сроков ведется в обратном порядке - от завершающий к исходной, как и В сетевом графике "вершины - события". У завершающей работы позднее и раннее окончание совпадают и отражают продолжительность критического пути. Позднее начало последующей работы равно позднему окончанию предыдущей. Если за данной работой следует несколько работ, то определяющим является минимальное значение из поздних начал.

Сетевые графики "вершины - работы" появились позже графиков "вершины - события", поэтому они несколько менее известны и сравнительно реже описываются в учебной и справочной литературе. Тем не менее, они имеют свои преимущества, в частности их легче строить и легче корректировать. При корректировка графиков ''вершены — работы" их конфигурация не меняется, у графиков же "вершины - события" такие изменения исключить не удается. Однако в настоящее время составление и корректировка сетевых графиков автоматизированы, и для пользователя, которому важно знать лишь последовательность работ и их резервы времени, не имеет особого значения, каким способом сделан график, т.е. какого он типа. В современных специализированных пакетах компьютерных программ планирования и оперативного управления в основном используется тип "вершины - работы".

Корректировка сетевых графиков производится как на этапе их составления, так и использования. Она состоит в оптимизации строительных работ по времени и по ресурсам (в частности по движению рабочей силы). Если, например, сетевой график не обеспечивает выполнения работ в необходимые сроки (нормативные или установленные контрактом) производится его корректировка по времени, т.е. сокращается продолжительность критического пути. Обычно это делается

за счет резервов времени некритических работ и соответствующего перераспределения ресурсов

за счет привлечения дополнительных ресурсов

за счет изменения организационно-технологической последовательности и взаимосвязи работ.

В последнем случае у графиков "вершины - события" приходится менять их конфигурацию (топологию).

Корректировка по ресурсам производится путем построения линейных календарных графиков по ранним началам, соответствующих тому или иному варианту сетевого графика, и корректировки этого варианта.

Автоматизированные системы управления строительством обычно включают компьютерные программы, в той или иной мере автоматизирующие практически все этапы составления и корректировки сетевых графиков.