Ошибка выборки.

Задача выборочного наблюдения – дать верное представление о сводных показателях всей совокупности факторов на основе некоторой части их подвергнутые обследованию. Поскольку речь идет о варьирующих признаках и изучается не вся совокупность единиц, а только часть их, то можно заранее сказать, что сводные показатели по этим признакм у части единиц совокупности почти никогда не будут абсолютно совпадать со сводныи показателями всех единиц совокупности.

Возможные пределы отклонений выборочной доли и выборочной средней от доли и средней генеральной совокупности носят название ошибки выборки, чем больше величина этой ошибки, тем в большей степени свободные показатели выборочного наблюдения отличается от сводных показателей всей совокупности.

Формула средней ошибки выборки имеет следующий вид:

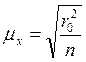
где, μ_x - средняя ошибка выборочной средней

r²₀ – дисперсия варьирующего признака в генеральной совокупности

n – численность единиц выборочной совокупности

Средняя ошибка выборочной доли определяется:

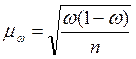; ω – доля признака

Выборка может проводиться по 2-ум схемам:

1. Схема повторной выборки – когда единица совокупности, попавшая в выборку после регистрации снова возвращается в генеральную совокупность, и она сохраняет равную возможность при отборе других единиц вновь попасть в выборку.

2. Схема бесповторной выборки – при которой единица совокупности, попавшая в выборку в дальнейшем уже в выборке не участвует.

Для бесповторной выборки формулы средней ошибки выборки принимают следующий вид:

Возможные значения генеральной средней и генеральной доли определяется по формулам: x¯=x+ μ_x; Р=ω+ μ_ω

В математической статистике доказано, что утверждение о том, что генеральные характеристики не отклоняются от выборочных на величину большую, чем величина ошибки выборки, всегда имеет постоянную степень вероятности равную 0,683 тыс. Значит с определенной степенью вероятности мы можем утверждать, что отклонение выборочных характеристик от генеральных не превысит некоторой величины, которая называется предельной ошибкой выборки.

Предельная ошибка выборки связана со средней ошибкой следующим равенством: ∆=t×μ, где t – коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка выборки не превысит t кратную среднюю ошибку.

Т.о. показатели x¯ и генеральной совокупности по показателям выборочной совокупности определяются:

x¯=x± t×μ_x Р= ω± t×μ_ω

x-t×μ_x ≤x¯≤ x+t×μ_x