СД типа граф.

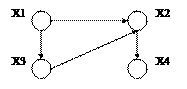
Граф – двойка G = (X, U), где X – множество элементов (вершин, узлов), а U представляет собой бинарное отношение на множестве X (U Í X´X). Если |X| = n (конечно), то граф является конечным. Элементы U называют либо дугами, либо ребрами.

		X = {X1, X2, X3, X4} X´X = {(X1,X1), …,(X4,X4)} U = {(X1,X2), (X1,X3), (X2,X3), (X2,X4)} Þ U Í X´X = X2

Если (X_i, X_j) – упорядоченная пара, то такой граф называется ориентированным (орграфом), а элементы U называются дугами. Если (X_i, X_j) = (X_j, X_i), то граф – неориентированный (неорграф), а элементы U называются ребрами.

F: U ® R – если задана такая функция, то граф является взвешенным, где R – множество вещественных чисел, т.е. отображение дуги на число.

Вообще: Æ U Í X × X.

Компонентами орграфа являются: дуга, путь, контур. Путь – такая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом последующей. Контур – конечный путь, у которого начальная вершина совпадает с конечной. Контур единичной длины называют петлей.

			G = G1 U G2

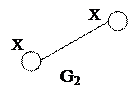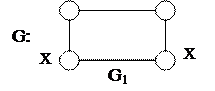Слабая связность – орграф заменяется неориентированным графом, который в свою очередь является связным. Односторонняя связность – это такая связность, когда между двумя вершинами существует путь в одну или в другую сторону. Сильная связность – это связность, когда между любыми двумя вершинами существует путь в одну и в другую сторону.