
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм прямого слияния.
Этот алгоритм является одним из простейших.

Серия – упорядоченная последовательность. Серия может быть различной длины.
Алгоритм:
1. Последовательность а разбивается на две половины b и c. Затем осуществляется слияние частей b и c, при этом серия размерностью 1 становится серией размерностью 2.
2. Полученная последовательность снова обрабатывается последовательностью 1 и 2. Получается серия размерностью 4.
3. Повторяем шаги, получая серии 8, … до тех пор, пока не будет упорядочена вся последовательность.
Рассмотренный алгоритм еще называют трехленточным (каждый файл последовательного доступа называют лентой).
a = {50, 3, 7, 60, 80, 90, 13, 15}
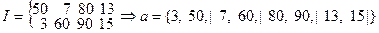


Поскольку на каждом проходе размерность серии удваивается, то сортировка заканчивается, когда p ³ n, где р – размер серии, а n – размер исходного файла.
Количество проходов: k = [log 2 n]. По определению при каждом проходе все множество из n элементов копируется ровно 1 раз, следовательно общее число пересылок М = n[log 2 n]. Число сравнений С еще меньше, чем М, т.к. при копировании остатка последовательности сравнения не производятся. Поскольку сортировка слиянием использует ВЗУ, то временные затраты на операцию пересылки на несколько порядков превышают временные затраты на операции сравнения.
Улучшение характеристик сортировки можно обеспечить увеличением файлов на фазе разделения и фазе слияния. Обозначим количество файлов – N. Тогда слияние r серий при 1 проходе дает r/N – количество серий, а на k-том проходе r/Nk. Тогда количество проходов будет k = [log N n], а количество пересылок М = n[log N n].
Например, при N=4:
| ¥ | - 1 | ||
| ¥ | - 2 | ||
| ¥ | - 3 | ||
| ¥ | - 4 |
| ¥ | |||||||||||||||||
| ¥ | ||||||||||||||||||
| ¥ | ||||||||||||||||||
| ¥ |
Вообще можно считать, что имеется N/2 входов и столько же выходов, и они меняются местами после каждого отдельного прохода.
Дата добавления: 2015-04-18; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |


