
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многофазная сортировка.
В основе данной сортировки лежит отказ от жесткого понятия прохода и разделения файлов на две категории. Рассмотрим этот метод сортировки на примере:
| |||||||
 |  |  | |||||
  f1 f1
| f2 | f3 | L | 
| 
| S | |
    13 13
| L=6 | ||||||
    5 5
| L=5 | ||||||
    0 0
| L=4 | ||||||
    3 3
| L=3 | ||||||
    1 1
| L=2 | ||||||
    0 0
| L=1 | ||||||
| L=0 |
Таким образом, необходимо, чтобы числа начальных серий в двух входных последовательностях были двумя соседними числами Фибоначчи.
        f1 f1
| f2 | f3 | f4 | f5 | f6 | L | 
| 
| 
| 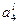
| 
| S | |
       16 16
| L=5 | ||||||||||||
       8 8
| L=4 | ||||||||||||
       4 4
| L=3 | ||||||||||||
       2 2
| L=2 | ||||||||||||
       1 1
| L=1 | ||||||||||||
| L=0 |
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Подставляя  вместо
вместо  , получаем
, получаем
 (для i ³ 4);
(для i ³ 4); 
Такие числа называются числами Фибоначчи четвертого порядка. В общем случае числа Фибоначчи порядка р определяются следующим образом:
 (для i > p);
(для i > p);  .
.
Заметим, что обычные числа Фибоначчи – числа первого порядка.
Теперь уже ясно, что исходные числа серий для идеальной многофазной сортировки с N последовательностями (файлами) представляют собой последовательность чисел Фибоначчи порядка N – 2. Отсюда следует, что метод применим для лишь входов, сумма серий на которых есть сумма N – 1 таких чисел Фибоначчи. В том случае, когда сумма серий отличается от идеальной суммы, то вводим фиктивную серию.
Дата добавления: 2015-04-18; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |


 Если
Если  , то
, то
 .
.
 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,…
0, 1, 1, 2, 3, 5, 8, 13, 21, 34,…