Оптимальные деревья поиска. Эффективность их применения. Алгоритм построения оптимального дерева поиска.

Во всех наших рассуждениях по поводу организации деревьев поиска до сих пор исходили из предположения, что частота обращения ко всем вершинам одинакова, т. е. все ключи с одинаковой вероятностью рассматриваются как аргументы поиска. Если нет других, то такое предположение является разумным. Но встречаются ситуации, когда есть информация о вероятности обращения к отдельным ключам. Обычно для таких ситуаций характерно постоянство множества ключей, т. е. в дерево не включаются новые ключи и не исключаются старые. Структура дерева остаётся неизменной Типичный пример – сканер транслятора, определяющий не относится ли каждое слово исходного текста программы к классу ключевых для данного языка программирования.

Статистические измерения для 100 программ могут дать точную информацию об относительных частотах появления отдельных ключей.

Пусть - вероятность обращения к k – й вершине дерева , . Надо так организовать дерево поиска, чтобы общее число шагов поиска, подсчитанное для достаточно большого числа обращений было минимальным. С этой целью принимаем в определении длины пути каждой вершины некоторый вес, который равен вероятности .

Условимся, что корень находится на уровне 1. Тогда средняя длина (среднее значение) пути всего дерева представляет собой сумму всех путей от корня к каждой вершине, умноженной на вероятность обращения к этой вершине.

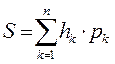
где h _k – уровень вершины k.

Цель – минимизировать среднее значение l _ср.

Пример.

Задано множество ключей {k _i} {1 , 2 , 3}, n = 3, , ,

Количество бинарных деревьев, которые можно построить из n узлов вычисляется по формуле:

Приблизительное равенство верно при n ³ 10.

a) d)

b) e)

c)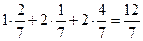

При данном распределении вероятностей лучшим является вырожденный вариант ( вариант а ).

Сканер транслятора требует ставить задачу в более общих условиях, ведь слова, встречающиеся в исходном тексте не всегда являются ключевыми.

Обнаружение, что данное слово не является зарезервированным, можно считать обращением к некоторой специальной вершине.

Если известна вероятность g _j того, что аргумент поиска х находится между двумя ключами k _j и k _{j + 1} , эта информация существенно трансформирует структуру дерева оптимального поиска.

Обобщим задачу: учтём неудачный поиск. Средняя длина пути в этом случае

- средняя длина пути

( * )

Специальная вершина обозначается квадратом и существует для всех пустых поддеревьев. Все эти специальные вершины являются внешними, остальные узлы – внутренними.

h_i – уровень внутренних вершин, который начинается с 1.

- уровень внешних вершин, который начинается с 0.

Эту среднюю длину пути Р называют ценой дерева поиска, т. к. она представляет некоторую меру поиска ожидаемых затрат. Дерево поиска, имеющее минимальную для всех деревьев, заданных множеством ключей {k _i} и вероятностями p_i и g _j, где будет находиться специальная вершина, называется оптимальным деревом.

Вместо вероятностей p_i и g _j мы будем использовать счётчики частоты обращений. Введём переменные a_i – число поисков с аргументом x = k _i;

b _j - число поисков с аргументом х , лежащим между ключами k _j и k _{j + 1}.

b ₀ – число поисков с аргументом x < k ₁

b _n – число поисков с x > k _n

взвешенная длина пути дерева.

Учитывая, что число возможных конфигураций из n вершин растёт экспоненциально, задача построения оптимального дерева методом перебора является безнадёжной. Воспользуемся принципом: любое поддерево оптимального дерева оптимально. Этот принцип подсказывает вычислительную процедуру, с помощью которой находится всё большие и большие оптимальные поддеревья, таким образом дерево растёт от листьев к корню.

В основе этого алгоритма лежит следующее уравнение

P = P _L + W + P _R ,

W – общее количество поисков, вес дерева

P _L – взвешенная длина пути левого поддерева

P _R – взвешенная длина пути правого поддерева.

Пример.

Р = 8*1 + 5*2 + 3* 3 = 5*1 + 3*2 + 8 + 5 + 3 P = P _L + W

P _L W

Пусть теперь T _{i j} - оптимальное поддерево , состоящее из вершин

k _{i + 1} , k _{i + 2} , … , k _j и частот a _{i + 1} , a _{i + 2} , … , a _j ;

b _i , b _{i + 1} , … , b _j

T _{o n} - всё дерево

W _{o n} - вес всего дерева

P _{o n} - взвешенный путь всего дерева

W _{i j} - общее число поисков для этого поддерева

P _{i j} - взвешенный путь для поддерева ( i j )

0 £ i < j £ n

При начальных условиях W_ii = b_i, 0 £ i £ n

T _{i i} имеет только специальные вершины.

P _{i i} = 0, 0 £ i £ n

W _{i j} = W _{i j – 1} + a _j + b _j, 0 £ i < j £ n

O( n ³ ) - сложность вычисления P _{i j} .