
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы сферической тригонометрии
Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников (например, на поверхности Земли и на небесной сфере).Сферические треугольники. На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности. Сторонами a, b, c сферического треугольника называют те углы между лучами, которые меньше 180 (если один из этих углов равен 180, то сферический треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга на поверхности шара (см. рисунок).

Углы A, B, C сферического треугольника, противолежащие сторонам a, b, c соответственно, представляют собой, по определению, меньшие, чем 180, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лучами.Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360, сумма углов заключена между 180 и 540. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180 плюс третий угол.Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):1) тремя сторонами, 2) тремя углами, 3) двумя сторонами и заключенным между ними углом, 4) стороной и двумя прилежащими к ней углами.
4)Формула косинуса стороны.
Формула косинуса стороны связывает три стороны и один из углов сферического треугольника. Удобна для нахождения неизвестного угла или стороны, противолежащей этому углу, и читается следующим образом: «в сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих сторон на косинус угла между ними»
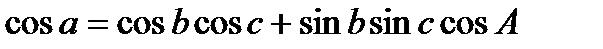
Дата добавления: 2015-04-18; просмотров: 366; Мы поможем в написании вашей работы!; Нарушение авторских прав |