
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямолинейно-параллельное вытеснение нефти водой
При поршневом вытеснении нефти водой в пористой среде плотности нефти и воды будем считать одинаковыми. Это позволит рассматривать плоскость контакта нефти и воды вертикальной. А различие в вязкостях нефти  и воды
и воды  будем учитывать.
будем учитывать.
В случае прямолинейно-параллельного движения схема вытеснения представлена на (рис.1.2.1). На контуре питания и на галерее поддерживаются соответствующие постоянные давления Рк и Рг. Начальное положение контура нефтеносности X0 параллельно галерее и контуру питания.
Обозначим через Xв текущее расстояние до контура нефтеносности в момент времени t после начала вытеснения, через Lk - расстояние от контура питания до галереи, через Рв и Рн давление в любой точке водоносной и нефтеносной части пласта соответственно, через Р(t)- давление на границе раздела вода – нефть, отстоящей от контура питания на расстояние Xв.
| Вода Нефть |
| h |
| B |
| 0 X0 Xв(t) Lk |
| x |
| Вода Нефть |
| РГ |
| РК |
| Р(t) |
Рис.1.2.1. Схема модели пласта при прямолинейно-параллельном движении границы раздела вода-нефть
Вспомним, что в случае установившегося прямолинейно-параллельного фильтрационного потока одной жидкости распределения давления и скорости фильтрации описываются следующими уравнениями:
 (1.2.1)
(1.2.1)
 , (1.2.2)
, (1.2.2)
где:
Р - давление в произвольной точке x, Па;
Рк - давление на контуре питания, Па;
Рг - давление на галерее, Па;
Lк - длина пласта, м.
При этом изобарами являются линии, параллельные галерее, и каждую изобару можно рассматривать как контур питания или как галерею. На основании формул (1.2.1) и (1.2.2) распределение давления и скорость фильтрации в водоносной области можно записать в виде:

 (1.2.3)
(1.2.3)
 , (1.2.4)
, (1.2.4)
где:
 - скорость фильтрации воды, м/с.
- скорость фильтрации воды, м/с.
Принимая за контур питания изобару, совпадающую с границей раздела жидкостей. Распределение давления и скорость фильтрации в нефтеносной области можно записать следующим образом:

 ; (1.2.5)
; (1.2.5)
 , (1.2.6)
, (1.2.6)
где:
 - скорость фильтрации нефти, м/c.
- скорость фильтрации нефти, м/c.
Найдем давление Р(t) на границе раздела. Вследствие не сжимаемости жидкостей и неразрывности потока линии тока будут иметь вид прямых, параллельных оси 0x (на границе раздела преломления не будет), а скорость фильтрации во всех точках пласта будет одинаковой, т. е.  .
.
Тогда из уравнений (1.2.4) и (1.2.6) получим:
 , (1.2.7)
, (1.2.7)
где:
 и
и  - динамическая вязкость воды и нефти соответственно, Па.с.
- динамическая вязкость воды и нефти соответственно, Па.с.
Откуда давление на границе раздела жидкостей будет равно:
 , (1.2.8)
, (1.2.8)
Определим теперь следующие характеристики фильтрационного потока нефти и воды:
1. Распределение давление в нефтеносной и водоносной областях. Для этого подставим (1.2.8) в (1.2.3) и (1.2.5):
 ; (1.2.9)
; (1.2.9)
 , (1.2.10)
, (1.2.10)
где:
РВ и РН – Давление в водоносной и нефтяной области соответственно, Па.
2. Скорость фильтрации. Подставим (1.2.8) в (1.2.4) и (1.2.6):
 . (1.2.11)
. (1.2.11)
3. Расход жидкости (дебит галереи) Q получается из (1.2.11) умножением на площадь сечения B.h:
 , (1.2.12)
, (1.2.12)
где:
B – Толщина пласта, м;
h – высота пласта, м;
Q – Установившейся дебит скважины,  .
.
4. Градиент давления. Продифференцируем (1.2.9) и (1.2.10) по X:
 ; (1.2.13)
; (1.2.13)
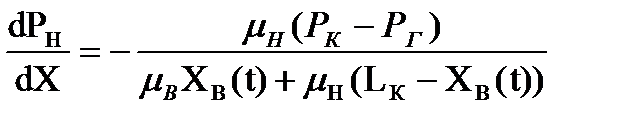 . (1.2.14)
. (1.2.14)
5. Закон движения границе раздела 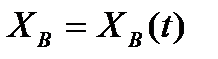 находим из соотношения скорости фильтрации и средней скорости движения:
находим из соотношения скорости фильтрации и средней скорости движения:
 , (1.2.15)
, (1.2.15)
откуда:
 , (1.2.16)
, (1.2.16)
где:
 - средняя скорость движения,
- средняя скорость движения,  ;
;
m – пористость, %;
t – время движения флюида, с.
Использовав (1.2.11), разделив переменные и проинтегрировав в пределах от 0 до t и от Х0 до ХВ, получим:
 (1.2.17)
(1.2.17)
Для того, чтобы найти время полного вытеснения нефти, нужно в формуле (1.2.16) положить Хв = L. Тогда получим:
 , (1.2.18)
, (1.2.18)
где:
Т – время полного вытеснения нефти, с.
Для нахождения зависимости координаты границы раздела XВ от времени t решим квадратное уравнение (1.2.16) относительно XВ:
 . (1.2.19)
. (1.2.19)
Подставив это значение XB формулы (1.2.11) и (1.2.12), найдем изменение скорости фильтрации и дебита галереи во времени:
 ; (1.2.20)
; (1.2.20)
 . (1.2.21)
. (1.2.21)
Проанализируем полученные характеристики потока.
1. Из уравнений (1.2.9) и (1.2.10) видно, что давление в пласте зависит не только от координаты X, но и от их положения границы раздела XВ. Но XВ, как следует это из формулы (1.2.19), со временем увеличивается, следовательно, пластовое давление во времени в водоносной области падает, а в нефтеносной растет. На (рис.1.2.2) показано распределение давления в пласте в начальный момент вытеснения, когда границы раздела занимают положение X0, и некоторое время t спустя, когда граница раздела продвинулась до положения XВ. Из графика видно, что пьезометрическая линия на границе раздела имеет излом.
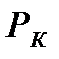
|
| Р, Па |
| X, м |

|

|

|

|

|
| djlf |
| Вода |
| Нефть |
Рис. 1.2.2. Кривые распределения давления в пласте при вытеснении нефти водой
2. Скорость Фильтрации  (1.2.20) и расход жидкости
(1.2.20) и расход жидкости  (1.2.21) также изменяются во времени. Следовательно, несмотря на пространство, депрессии
(1.2.21) также изменяются во времени. Следовательно, несмотря на пространство, депрессии  движение жидкостей в пласте будет неустановившимся.
движение жидкостей в пласте будет неустановившимся.
При  , как видно из указанных формул, скорость и дебит галереи увеличиваются с течением времени, т. е. по мере продвижения контура нефтеносности.
, как видно из указанных формул, скорость и дебит галереи увеличиваются с течением времени, т. е. по мере продвижения контура нефтеносности.
Это легко объяснимо и из физических соображений. Движение жидкостей в пласте происходит под действием постоянного перепада давления  . Величина же сопротивления, оказываемого обеими жидкостями, зависит от размеров их областей. С течением времени увеличивается область водоносности, сопротивление которой по сравнению с областью нефтеносности тех же размеров значительно меньше. Следовательно, общее сопротивление обеих областей во времени уменьшается, что при постоянной депрессии
. Величина же сопротивления, оказываемого обеими жидкостями, зависит от размеров их областей. С течением времени увеличивается область водоносности, сопротивление которой по сравнению с областью нефтеносности тех же размеров значительно меньше. Следовательно, общее сопротивление обеих областей во времени уменьшается, что при постоянной депрессии  ведет к росту скорости фильтрации и дебита галереи.
ведет к росту скорости фильтрации и дебита галереи.
3. Градиент давления в водоносной и нефтеносной областях, как это следует из формул (1.2.13) и (1.2.14) с учетом (1.2.19), увеличиваются во времени. Это же видно из (рис.1.2.2). В нефтеносной области градиент давления больше, чем в водоносной во столько раз, во сколько вязкость нефти больше вязкости воды.
Если первоначальное положение водонефтяного контакта АВ в пласте не параллельно галерее (рис.1.2.3), то решить задачу можно только приближенно, например, используя метод «полосок», предложенный В. Н. Щелкачевым.
| X, м |
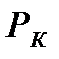
|
| В |
| А |

|

|

|

|
| Р, Па |
Рис.1.2.3. Схема использования метода «полосок»
В потоке выделяются узкие полоски, в пределах каждой из которых водонефтяной контакт считается параллельным галерее, и движение в каждой полоске описывается выведенными формулами. При этом, как видно из формулы (1.2.20), чем больше X0 , тем больше скорость фильтрации 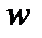 . Отсюда вытекает, что граница раздела в точке В будет двигаться гораздо быстрее, чем в точке А, и обводнение галереи начнется именно по линии
. Отсюда вытекает, что граница раздела в точке В будет двигаться гораздо быстрее, чем в точке А, и обводнение галереи начнется именно по линии  , в то время как контур нефтеносности по другим линиям будет еще значительно удален от галереи. Из этого примера следует важное заключение о характере продвижения контура нефтеносности. Если на границе раздела вода-нефть при разработке нефтяной залежи образовался «водяной язык», то он в дальнейшем не только не исчезнет, а быстро вытягивается, продвигаясь с большой скоростью, чем остальная часть водонефтяного контакта.
, в то время как контур нефтеносности по другим линиям будет еще значительно удален от галереи. Из этого примера следует важное заключение о характере продвижения контура нефтеносности. Если на границе раздела вода-нефть при разработке нефтяной залежи образовался «водяной язык», то он в дальнейшем не только не исчезнет, а быстро вытягивается, продвигаясь с большой скоростью, чем остальная часть водонефтяного контакта.
Дата добавления: 2015-04-18; просмотров: 340; Мы поможем в написании вашей работы!; Нарушение авторских прав |