
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 2. Расчетная часть
2.1. Исследование прямолинейно-параллельной установившейся фильтрации однородной несжимаемой жидкости по закону Дарси в однородном пласте (приток к галерее)
Задача №1
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит галереи, закон движения частиц жидкости и средневзвешенное по объему порового пространства пластовое давление при следующих исходных данных (см. табл. 2.1.1.).
Таблица 2.1.1
Исходные данные
| PK, МПа | PГ, МПа | LK, м | k ,мкм2 | μ, мПа.c | B, м | h, м | m, м |
| 9,5 | 8,5 | 0,5 | 2,5 |
где:
LК- длина пласта; B- ширина пласта; h- толщина пласта; m- пористость;
k- проницаемость; PK- давление на контуре питания; PГ давление на стенке галереи; μ- динамическая вязкость жидкости.
| Pк |
| Рг |
| В |
| h |
| LК |
Рис.2.1.1. Схема прямолинейно–параллельного фильтрационного потока в пласте.
Решение:
1) Определение закона распределения давления:
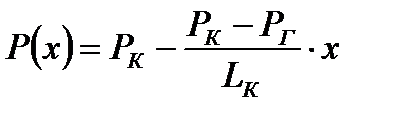 , (2.1.1)
, (2.1.1)
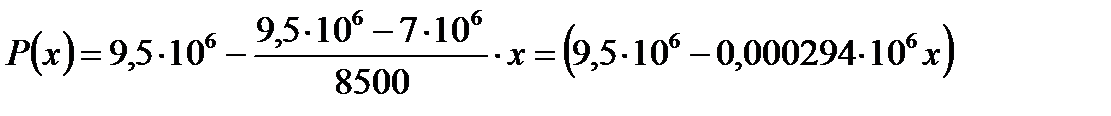 [Па];
[Па];
 [МПа].
[МПа].
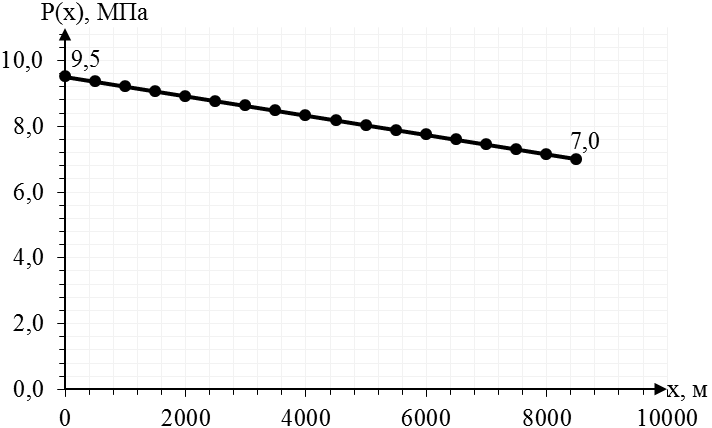
Рис.2.1.2. График распределения давления в пласте (пьезометрическая линия) Р(х)
2) Определение градиента давления:
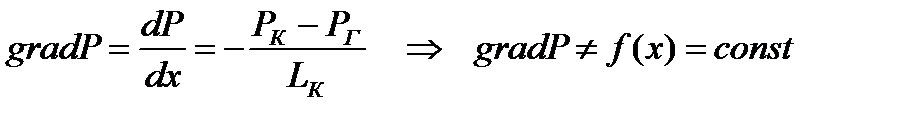 , (2.1.2)
, (2.1.2)
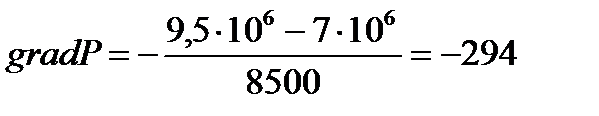 [Па/м].
[Па/м].
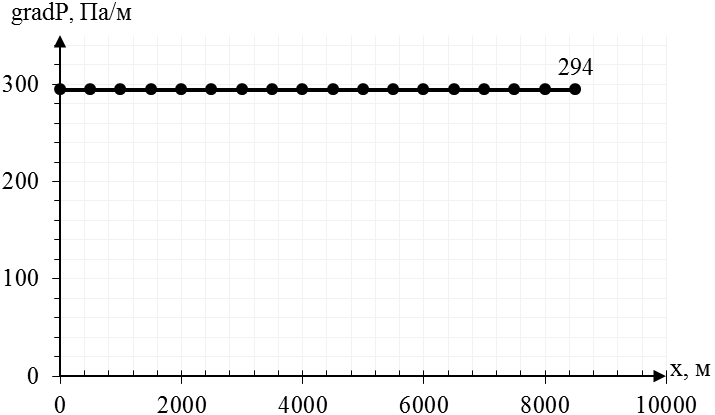
Рис.2.1.3. График распределения градиента давления в пласте 
3) Определение скорости фильтрации:
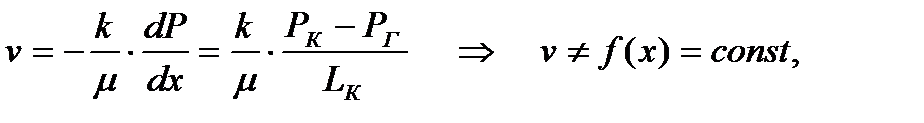 (2.1.3)
(2.1.3)
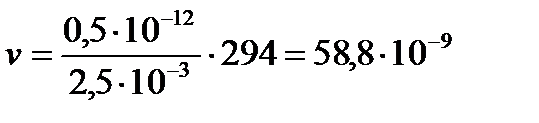 [м/с].
[м/с].
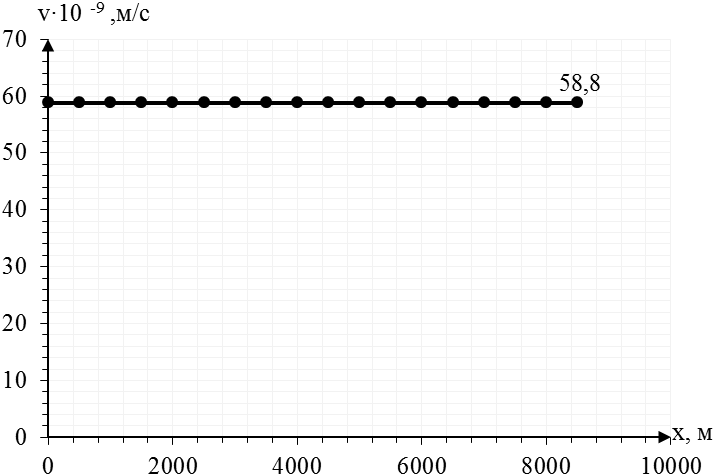
Рис.2.1.4.График распределения скорости фильтрации в пласте 
4) Определение дебита галереи:
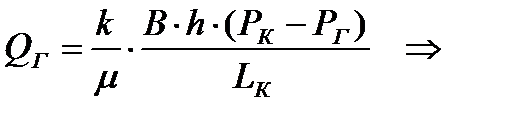
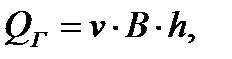 (2.1.4)
(2.1.4)
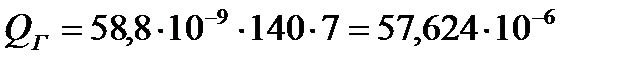 [м/с].
[м/с].
5) Определение закона движения частиц жидкости:
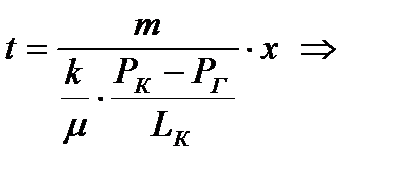
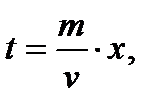 (2.1.5)
(2.1.5)
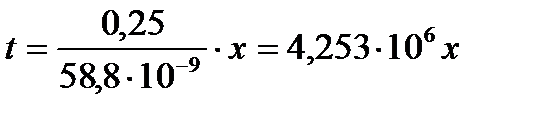 , [с].
, [с].
6) Средневзвешенное по объему порового пространства пластовое давление:
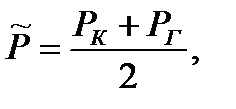 (2.1.6)
(2.1.6)
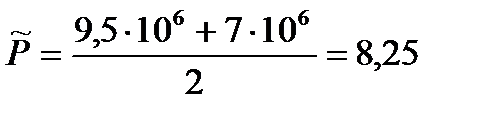 [МПа].
[МПа].
2.2. Исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном пласте (приток к совершенной скважине).
Задача №2
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит скважины, закон движения частиц жидкости и средневзвешенное по объему порового пространства пластовое давление при следующих исходных данных (см. табл. 2.2.1.).
Таблица 2.2.1
Исходные данные
| PK, МПа | PС, МПа | RK, м | rC, м | k ,мкм2 | μ, мПа.c | h, м | m, м |
| 9,5 | 0,2 | 0,5 | 2,5 |
где
PK - давление на контуре питания; PС - давление на забое скважины; RK - радиус контура питания; rC - радиус скважины;μ - динамическая вязкость жидкости; h- толщина пласта; m - проницаемость; μ - пористость.

Рис. 2.2.1.Схема плоскорадиального потока
Решение:
1) Определение закона распределения давления в пласте:
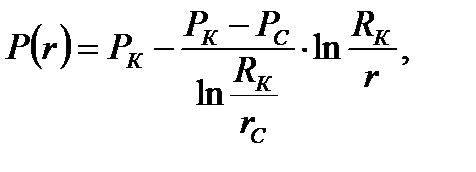 (2.2.1)
(2.2.1)
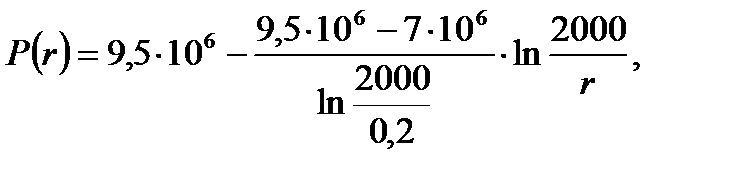
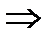
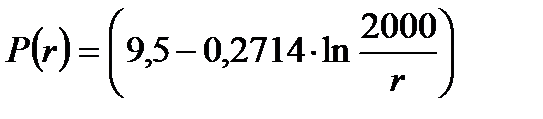 [МПа].
[МПа].
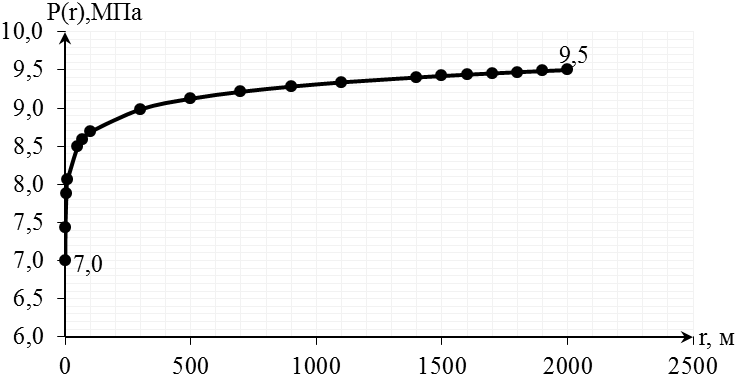
Рис.2.2.2. График распределения давления в пласте 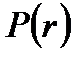
2) Определение градиента давления:
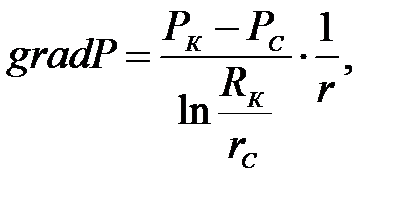 (2.2.2)
(2.2.2)
 [Па/м].
[Па/м].

Рис. 2.2.3. График распределения градиента давления в пласте 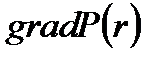
3) Определение скорости фильтрации:
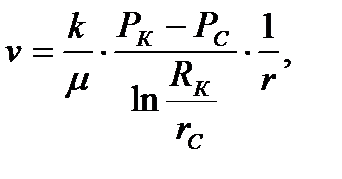 (2.2.3)
(2.2.3)
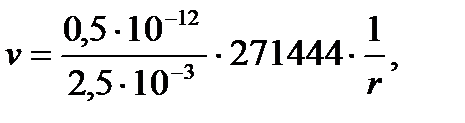
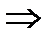
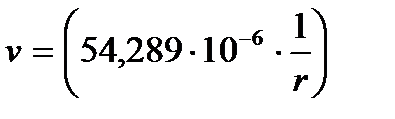 [м/с].
[м/с].
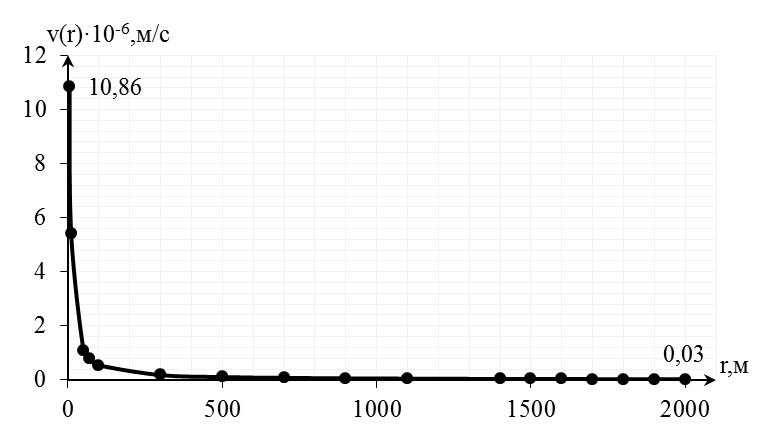
Рис. 2.2.4. График распределения скорости фильтрации 
4) Определение дебита скважины (по формуле Дюпюи):
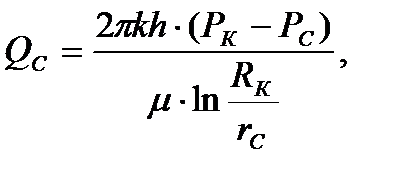 (2.2.4)
(2.2.4)
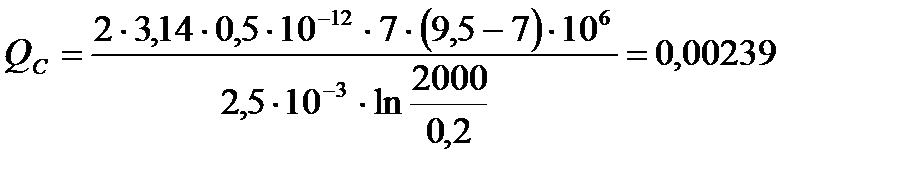 [м3/с].
[м3/с].
5) Определение закона движения частиц жидкости:
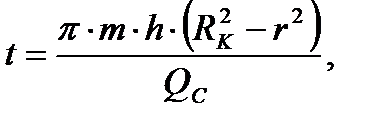 (2.2.5)
(2.2.5)
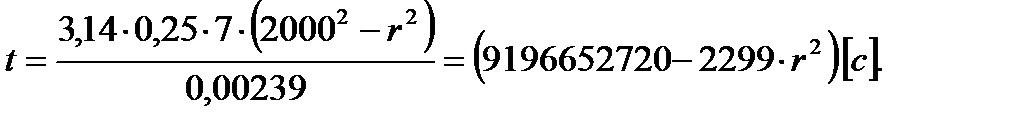
6) Средневзвешенное по объему порового пространства пластовое давление:
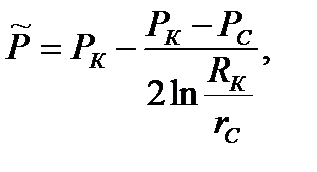 (2.2.6)
(2.2.6)
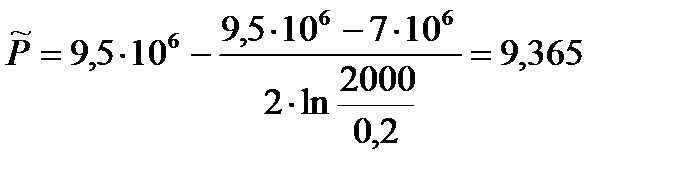 [МПа].
[МПа].
2.3. Исследование одномерного прямолинейно-параллельного установившегося фильтрационного потока несжимаемой жидкости в неоднородном пласте.
Задача №3
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит галереи и средний коэффициент проницаемости для двух случаев неоднородности пласта: слоисто-неоднородного и зонально-неоднородного - при следующих исходных данных (см. табл. 2.3.1.).
Таблица 2.3.1
Исходные данные

| 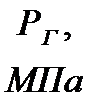
| 
| 
| 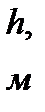
| 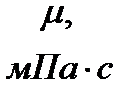
| Слоисто – неоднородный | Зонально – неоднородный | ||||||
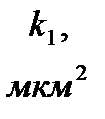
| 
| 
| 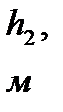
| 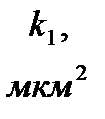
| 
| 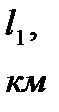
| 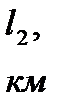
| ||||||
| 9,5 | 7,0 | 8,5 | 2,5 | 0,6 | 0,5 | 0,6 | 0,5 | 4,5 |
где:
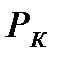 – давление на контуре питания;
– давление на контуре питания;
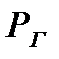 – давление на стенке галереи;
– давление на стенке галереи;
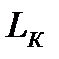 – длина пласта;
– длина пласта; 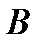 – ширина пласта;
– ширина пласта;
 – толщина пласта;
– толщина пласта;
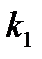 ,
, 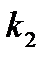 – проницаемость пропластков или зон пласта;
– проницаемость пропластков или зон пласта;
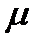 – динамическая вязкость жидкости;
– динамическая вязкость жидкости;
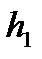 ,
, 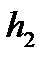 – толщина пропластков;
– толщина пропластков;
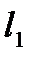 ,
, 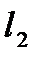 – длина зон пласта.
– длина зон пласта.

Рис. 2.3.1. Схема прямолинейно–параллельного фильтрационного потока в: а) слоисто-неоднородном, б) зонально-неоднородном пластах
Решение:
а) Слоисто-неоднородный пласт.
1) Определение закона распределения давления в пласте:
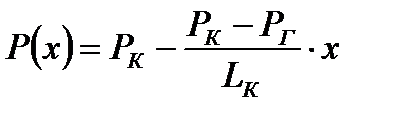 , (2.3.1)
, (2.3.1)
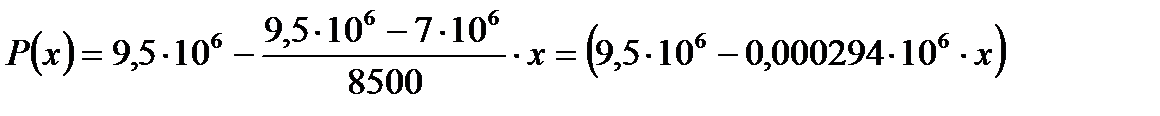 [Па]
[Па]
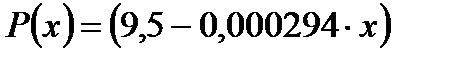 [МПа]
[МПа]

Рис.2.3.2. График распределения давления в пласте Р(х) (пьезометрическая линия)
2) Определение градиента давления:
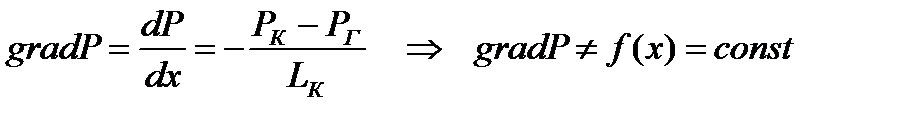 , (2.3.2)
, (2.3.2)
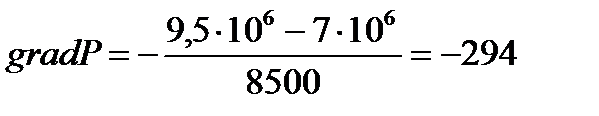 [Па/м].
[Па/м].
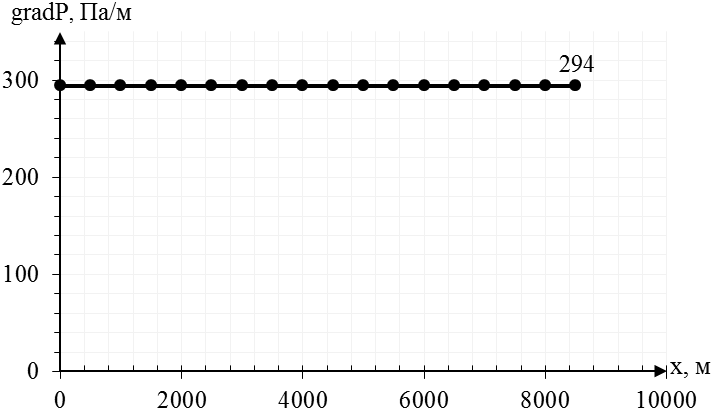
Рис.2.3.3.График распределения градиента давления в пласте 
3) Определение скорости фильтрации:
 (2.3.3)
(2.3.3)
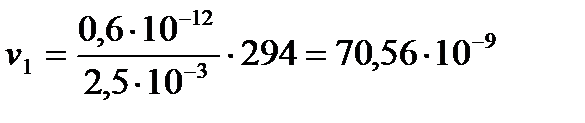 [м/с];
[м/с]; 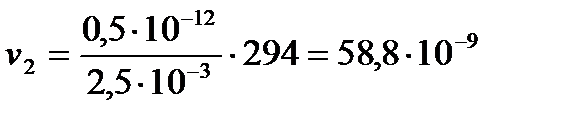 [м/с].
[м/с].
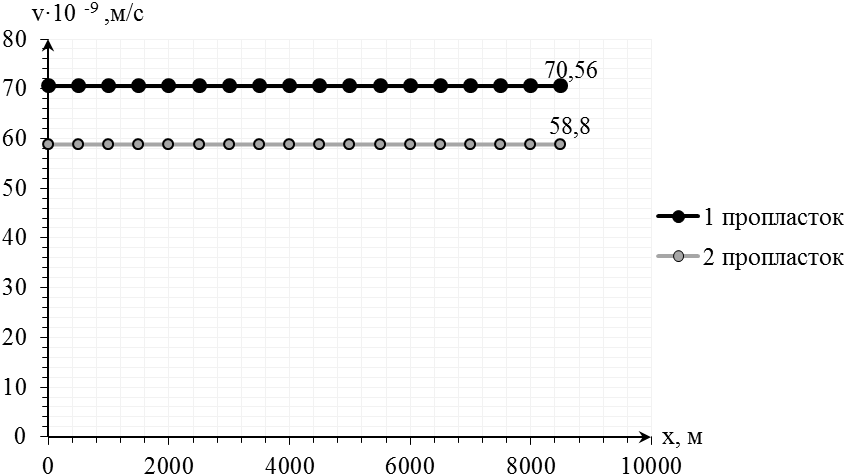
Рис. 2.3.4. График распределения скорости фильтрации в пласте 
4) Определение дебита галереи:
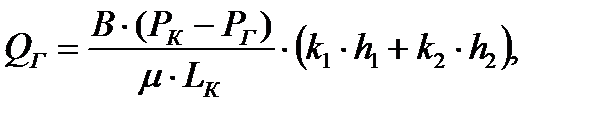 (2.3.4)
(2.3.4)
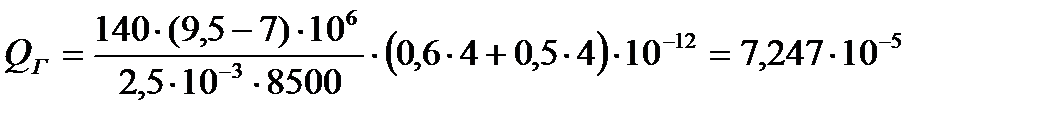 [м3/с].
[м3/с].
5) Определение средней проницаемости пласта:
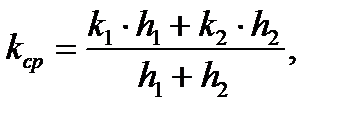 (2.3.5)
(2.3.5)
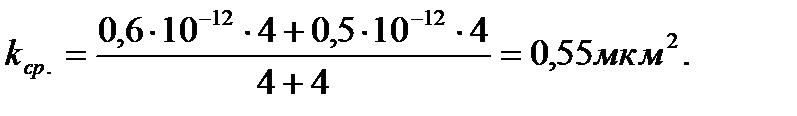
б) Зонально-неоднородный пласт.
1) Распределение давления в каждом из пропластков линейное, определяется следующими выражениями:
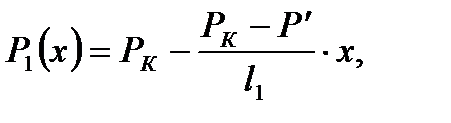 где
где  , (2.3.6)
, (2.3.6)
 где
где 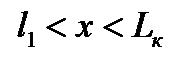 (2.3.7)
(2.3.7)
Для начала определяется давление на границе 1 и 2 зон, основываясь на уравнение неразрывности:
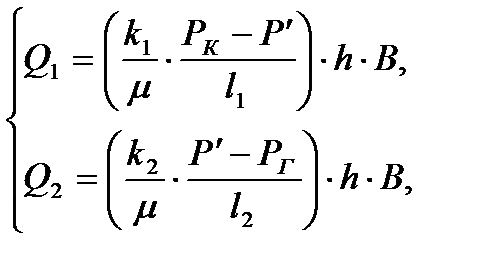
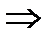
 (2.3.8)
(2.3.8)
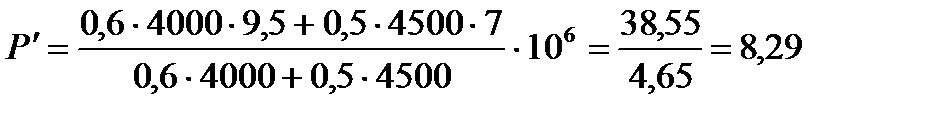 [МПа];
[МПа];
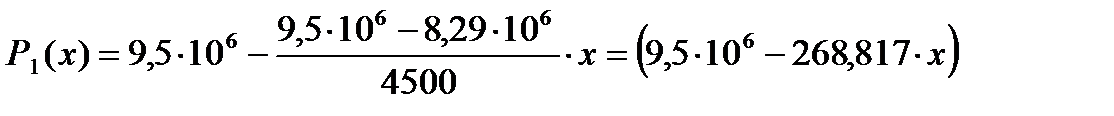 [Па];
[Па];
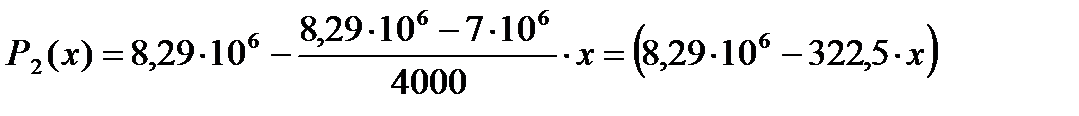 [Па];
[Па];
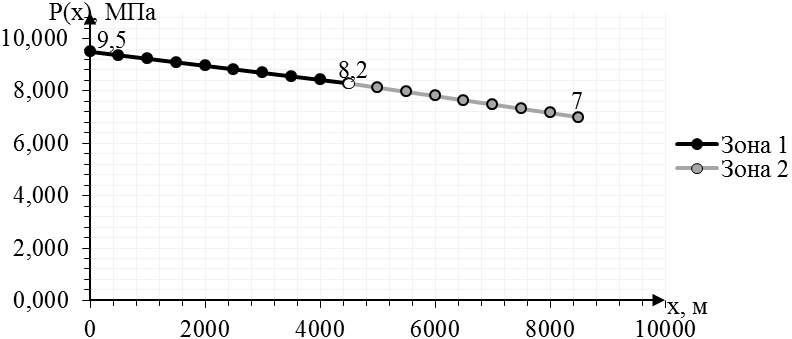
Рис. 2.3.5. График распределения давления в пласте 
2) Определение градиента давления:
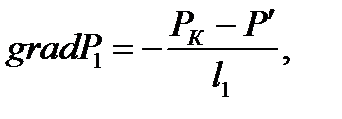 (2.3.9)
(2.3.9)
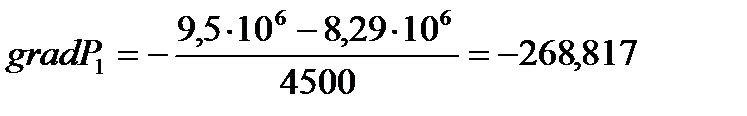 [Па/м];
[Па/м];
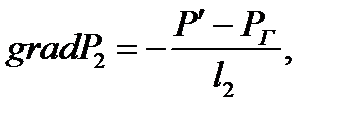 (2.3.10)
(2.3.10)
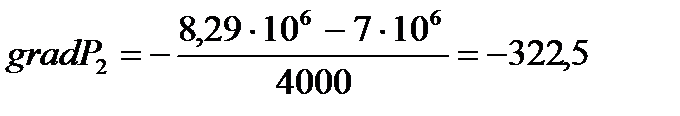 [Па/м].
[Па/м].
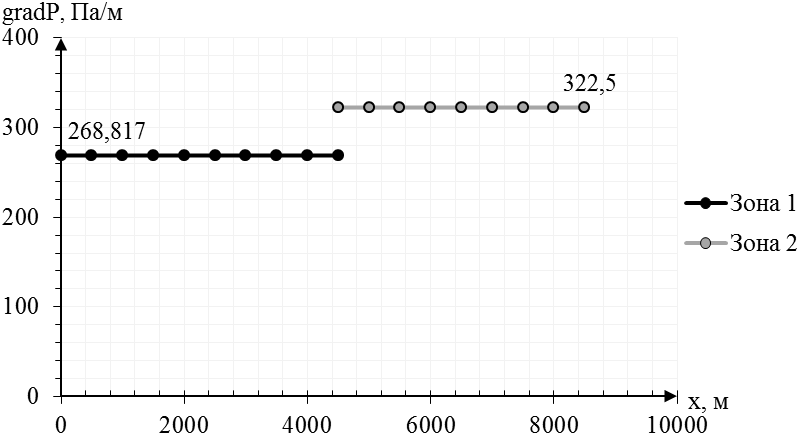
Рис. 2.3.6. График распределения градиента давления в пласте 
3) Определение скорости фильтрации:
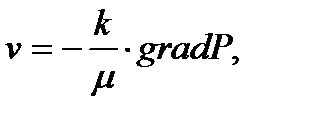 (2.3.11)
(2.3.11)
 [м/с];
[м/с];
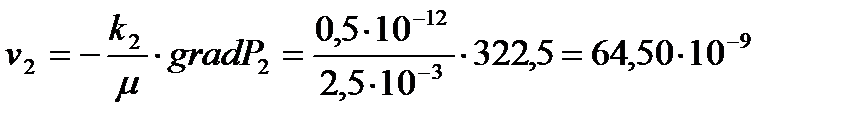 [м/с].
[м/с].
4) Определение дебита галереи:
Из уравнения неразрывности фильтрационного потока следует, что объемные расходы по зонам и по всей полосообразной залежи одинаковы, т.е.:
Q =v1F1= v2F2  (2.3.12)
(2.3.12)
т.к. F1=F2= 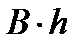 , то v1=v2.
, то v1=v2.
QГ=Q1= Q2=v1F1= v2F2 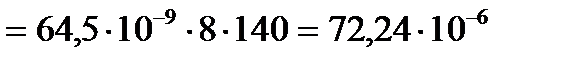 [м3/с].
[м3/с].
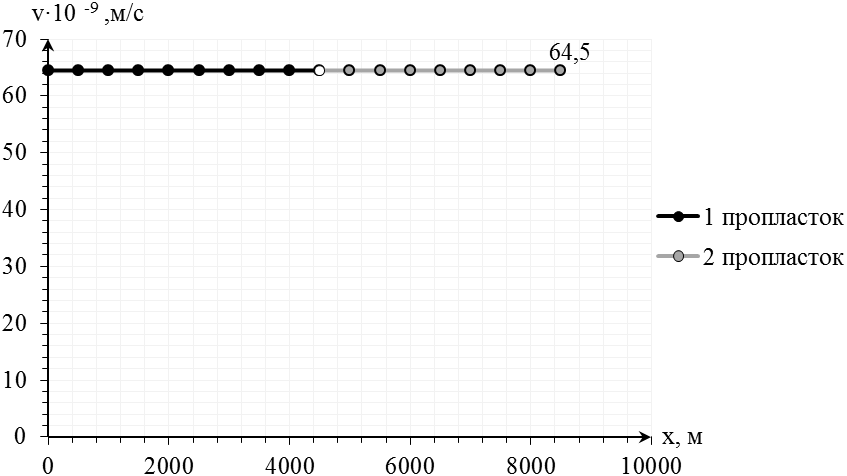
Рис.2.3.7. График распределения скорости фильтрации в пласте 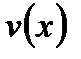
5) Определение средней проницаемости пласта:
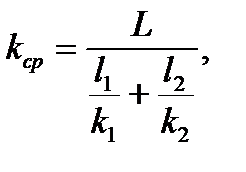 (2.3.13)
(2.3.13)
 [мкм2].
[мкм2].
2.4. Исследование одномерного плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородном пласте.
Задача №4
Определить закон распределения давления, градиента давления и скорости фильтрации по длине пласта (в математическом и графическом виде), дебит скважины и средний коэффициент проницаемости для двух случаев неоднородности пласта: слоисто-неоднородного и зонально-неоднородного - при следующих исходных данных (см. табл. 2.4.1).
Таблица 2.4.1
Исходные данные

| 
| 
| 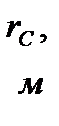
| 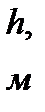
| 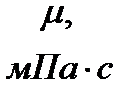
| Слоисто - неоднородный | Зонально - неоднородный | |||||
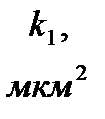
| 
| 
| 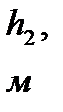
| 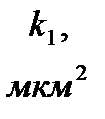
| 
| 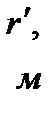
| ||||||
| 9,5 | 0,2 | 2,5 | 0,6 | 0,5 | 0,6 | 0,5 |
где 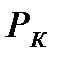 – давление на контуре питания;
– давление на контуре питания;
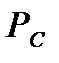 – давление на забое скважины;
– давление на забое скважины;
 – радиус контура питания;
– радиус контура питания;
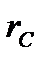 – радиус скважины;
– радиус скважины;
 – толщина пласта;
– толщина пласта;
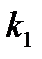 ,
, 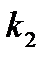 – проницаемость пропластков или зон пласта;
– проницаемость пропластков или зон пласта;
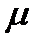 – динамическая вязкость жидкости;
– динамическая вязкость жидкости;
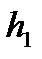 ,
, 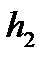 – толщина пропластков;
– толщина пропластков;
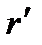 – радиус границы между первой и второй зонами пласта.
– радиус границы между первой и второй зонами пласта.

Рис.2.4.1. Схема плоскорадиального фильтрационного потока: а) слоисто-неоднородном, б) зонально-неоднородном пластах
Решение:
а) Слоисто-неоднородный пласт.
1) Определение закона распределения давления в пласте:
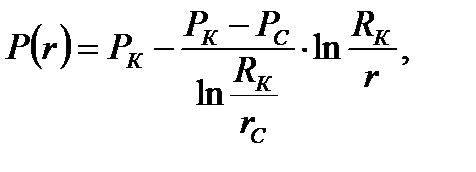 (2.4.1)
(2.4.1)
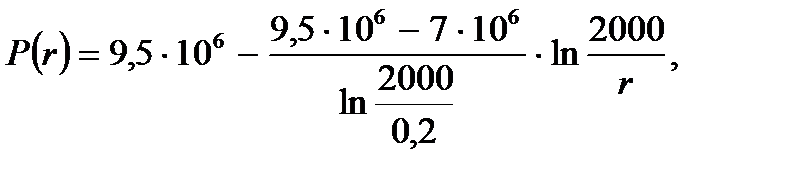
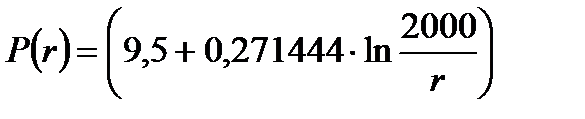 [МПа].
[МПа].
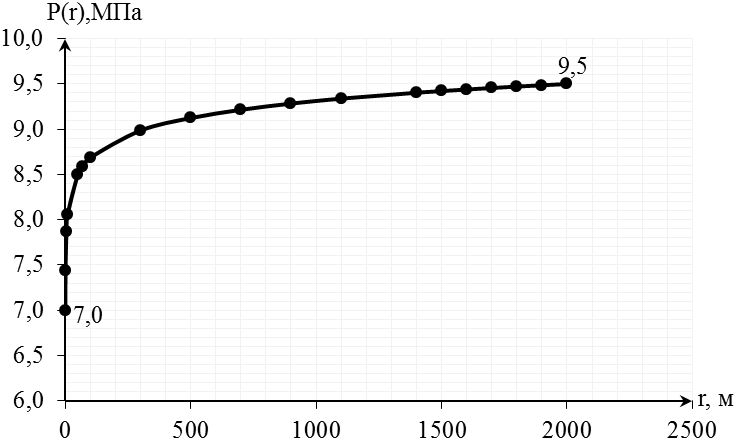
Рис.2.4.2. График распределения давления в пласте 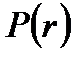
2) Определение градиента давления:
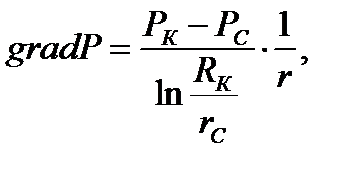 (2.4.2)
(2.4.2)
 [Па/м].
[Па/м].
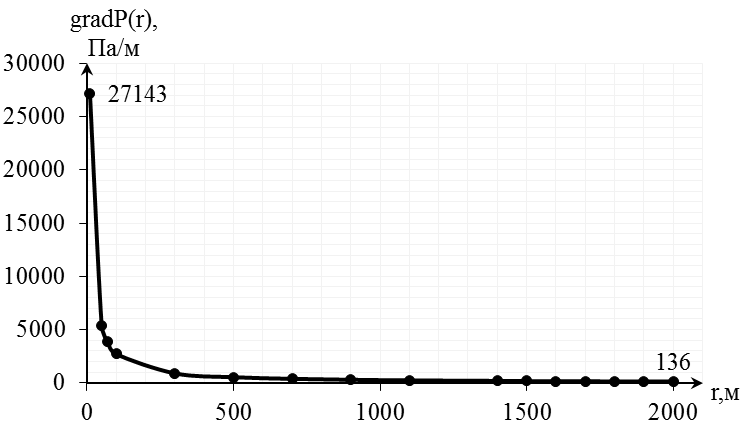
Рис.2.4.3. График распределения градиента давления в пласте 
3) Определение скорости фильтрации:
 (2.4.3)
(2.4.3)
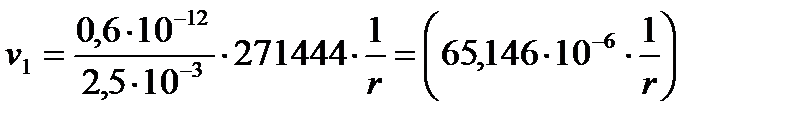 [м/с];
[м/с];
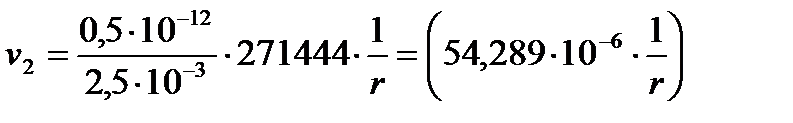 [м/с].
[м/с].
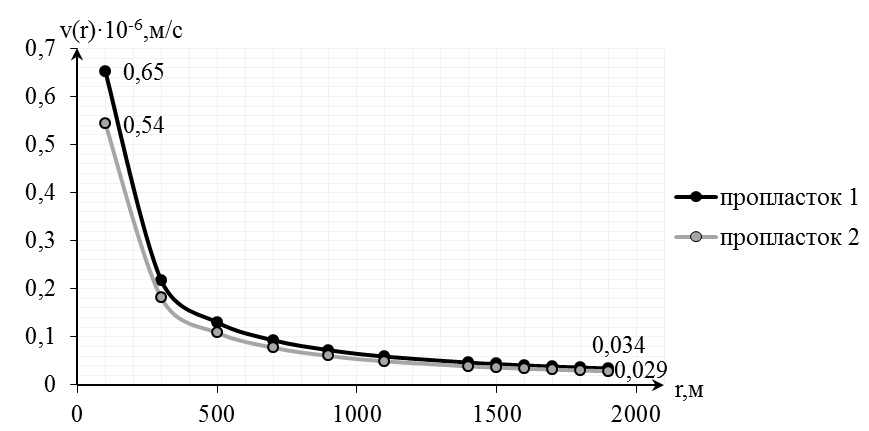
Рис.2.4.4.График распределения скорости фильтрации 
4) Определение дебита скважины:
Дебит потока Q можно вычислить как сумму дебитов в отдельных пропластах Q1 и Q2:
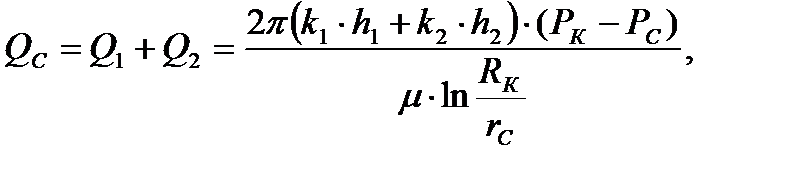 (2.4.4)
(2.4.4)
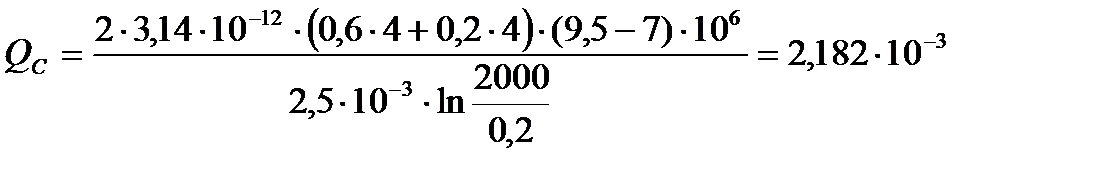 [м3/с].
[м3/с].
5) Определение средней проницаемости пласта:
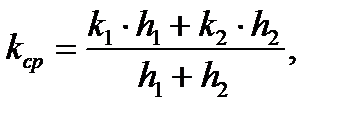 (2.4.5)
(2.4.5)
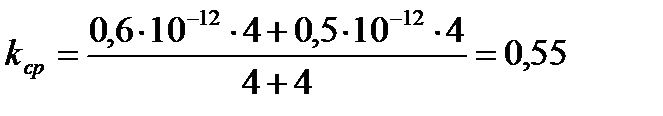 [мкм2].
[мкм2].
б) Зонально-неоднородный пласт.
Распределение давления в каждой из зон носит логарифмический характер и определяется выражениями:
 (2.4.6)
(2.4.6)
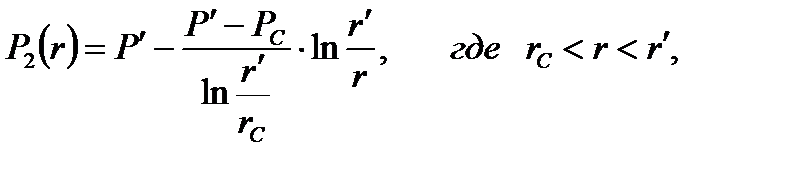 (2.4.7)
(2.4.7)
Для начала определяется давление 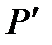 на границе между зонами, основываясь на уравнении неразрывности
на границе между зонами, основываясь на уравнении неразрывности 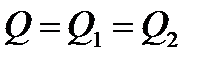 .
.
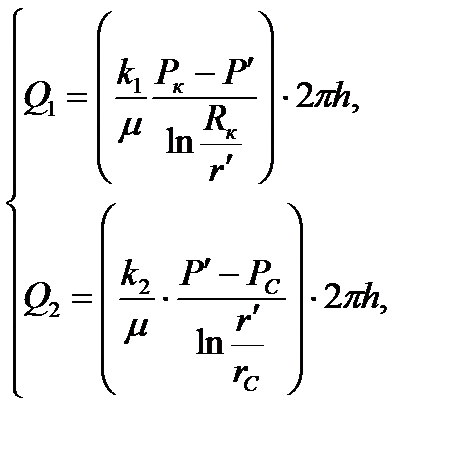
 (2.4.8)
(2.4.8)
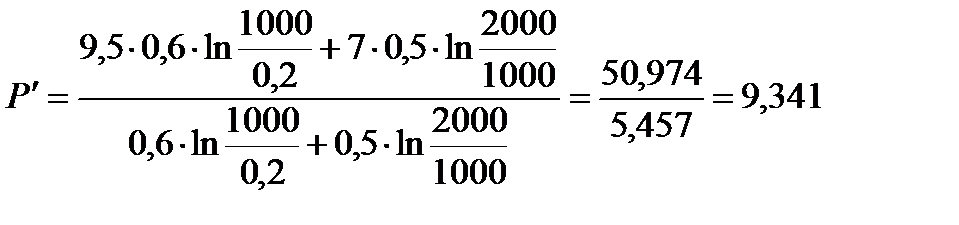 [МПа];
[МПа];
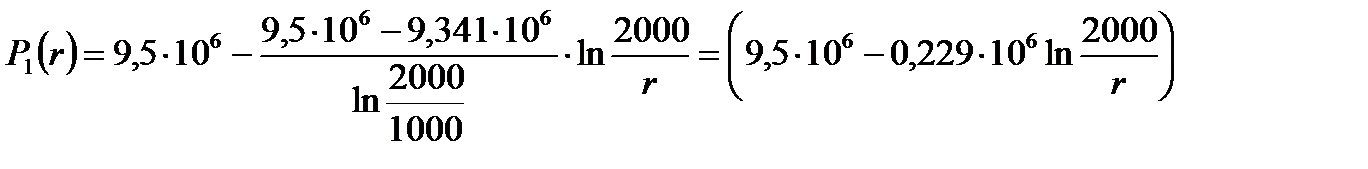 [Па];
[Па];
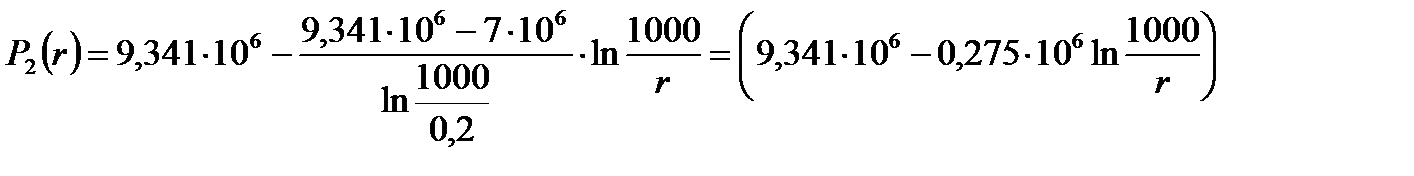 [Па].
[Па].
2) Определение градиента давления:
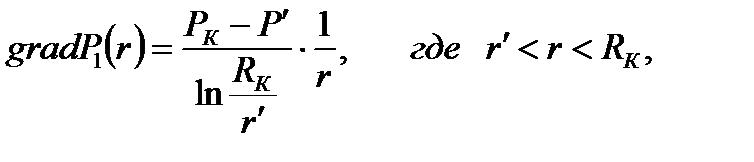 (2.4.9)
(2.4.9) 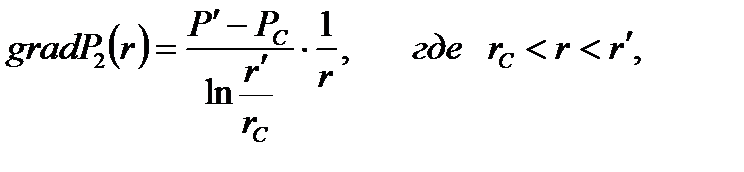 (2.4.10)
(2.4.10)
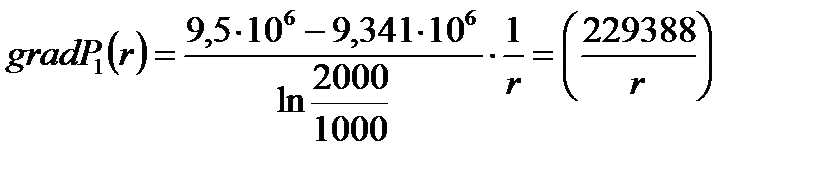 [Па/м];
[Па/м];
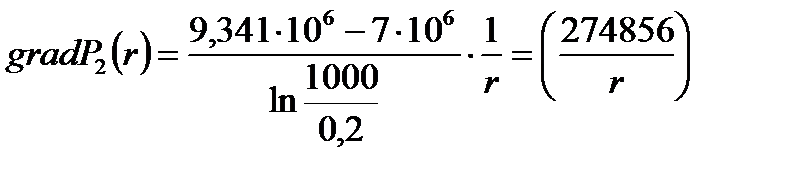 [Па/м].
[Па/м].

Рис.2.4.5. График распределения давления в пласте 
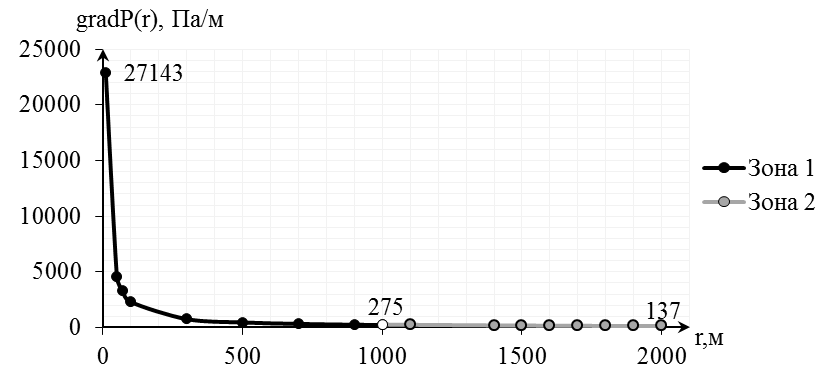
Рис.2.4.6. График распределения градиента давления в пласте 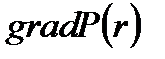
3) Определение скорости фильтрации:
 (2.4.11)
(2.4.11)
 [м/с];
[м/с];
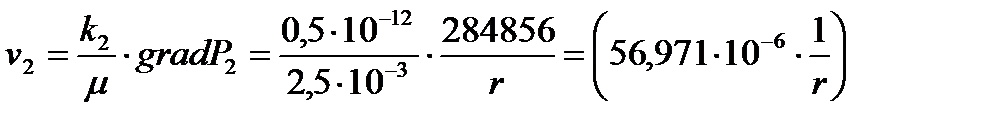 [м/с].
[м/с].
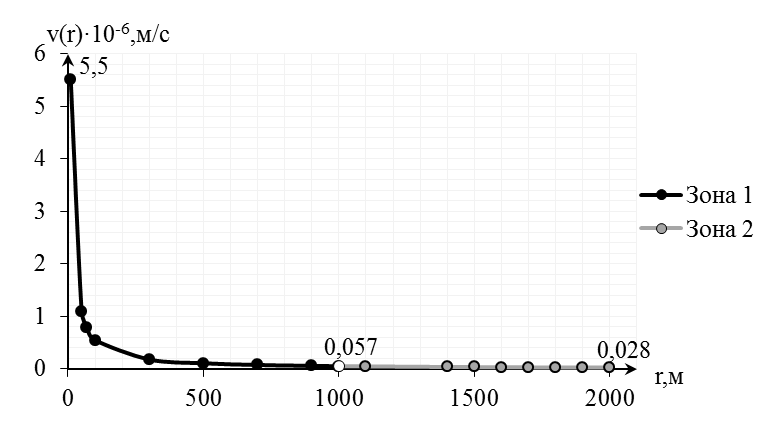
Рис.4.7.График распределения скорости фильтрации в пласте 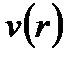
4) Определение дебита скважины:
 (2.4.12)
(2.4.12)
 [м3/с].
[м3/с].
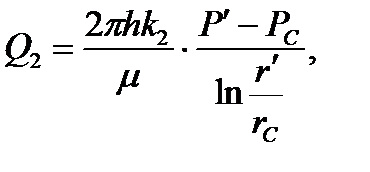 (2.4.13)
(2.4.13)
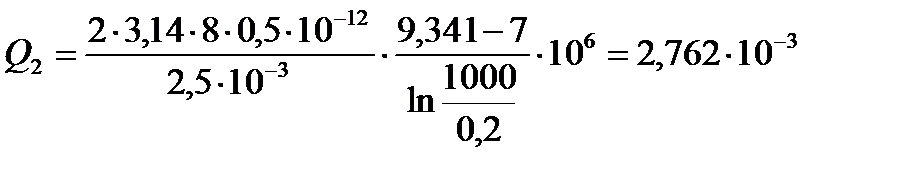 [м3/с].
[м3/с].
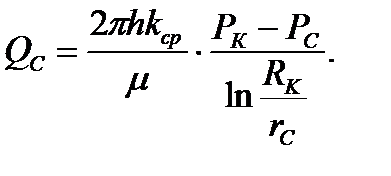 (2.4.14)
(2.4.14)
5) Определение средней проницаемости пласта:
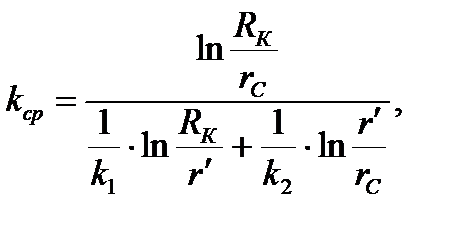 (2.4.15)
(2.4.15)
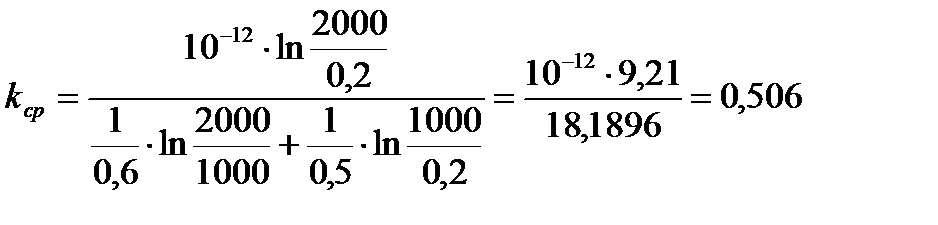 [мкм2];
[мкм2];
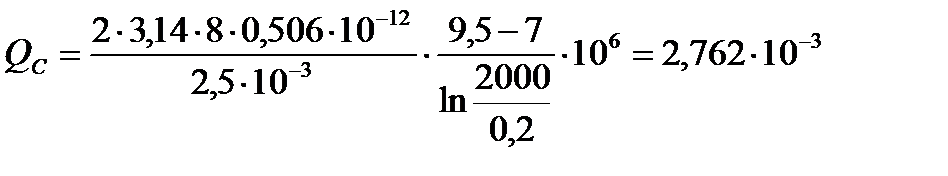 [м3/с].
[м3/с].
Заключение
В ходе курсовой работы была изучена теория «Расчёта параметров вытеснения одной жидкости другой».
Также был рассмотрен вопрос вытеснения одной жидкости другой являющийся наиболее важными, так как большинство нефтегазовых месторождений эксплуатируется при водонапорном и упруговодонапорном режиме работы залежи, а расчёт параметров вытеснения нефти водой позволяет рассчитать дебит нефти таких залежей.
Были рассмотрены расчеты на определение предельного безводного дебита скважин и предельно допустимой депрессии при отборе нефти из скважин, вскрывающих пласт с подошвенной водой.
Для решения практических задач разработки нефтяных и газовых месторождений важное значение, имеет прогнозирование продвижения контактов пластовых флюидов, а также контроль и регулирование динамики их перемещения. Это позволяет оптимизировать систему разработки месторождения, правильно определить число и размещение добывающих и нагнетательных скважин на месторождениях при естественных и искусственных режимах их эксплуатации.
В расчетной части были рассмотрены и проведены исследования прямолинейно-параллельного и плоскорадиального одномерного фильтрационного потока несжимаемой жидкости в однородных и неоднородных пластах. Была установлена зависимость распределения давления, градиента давления, скорости фильтрации в пласте.
По результатам работы и полученных результатов, можно сказать, что взаимодействие между скважинами достаточно большое, и, следовательно, на практике необходимо учитывать влияние скважин друг на друга, нельзя рассматривать каждую скважину в отдельности, без учета действия на неё других скважин и самого пласта, это может привести к увеличению погрешности расчетов.
Список литературы
1. Басииев К. С, Кочина И. Н., Максимов В. М. Подземная гидромеханика: Учебник для вузов.-М.: Недра, 1993. 416 с: ил.
2. Щелкачев В.Н., Лапук Б.Б. Подземная гидравлика. - М.: Гостоптехиздат, 2001. 525 с.
3. Рогачев М.К. Подземная гидромеханика. Лабораторный практикум. – СПб.: СПГГИ(ТУ), 2006. - 38 с.
Дата добавления: 2015-04-18; просмотров: 744; Мы поможем в написании вашей работы!; Нарушение авторских прав |