
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос № 39. Объясните понятие гидравлически гладких и шероховатых труб. Может ли одна и та же труба быть гидравлически гладкой и гидравлически шероховатой? В каком случае?
Потери напора по длине потока могут весьма существенно зависеть от характеристик шероховатости стенок трубы, в которых происходит движение. Поверхность стенок, ограничивающих поток, всегда отличается от идеально гладкой поверхности наличием выступов и неровностей. Величина и форма этих выступов зависят от материала стенки, от его обработки, условий эксплуатации, в процессе которой возможна коррозия, могут выпасть и осесть на стенках твердые частицы наносов и т.п. Стенки труб покрытые однородными бугорками со средней абсолютной высотой выступа шероховатости, обозначают Δ.
В зависимости от того, как относятся размеры выступов шероховатости и толщина ламинарной пленки, все трубы могут быть при турбулентном режиме движения подразделены на три вида.
Если высота выступов шероховатости Δ меньше, чем толщина ламинарной пленки (Δ <δ), то в этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости, а стенки называются гидравлически гладкими.
Когда высота выступов шероховатости превышает толщину ламинарной пленки (Δ <δ), то потери напора зависят от шероховатости, и такие трубы называются гидравлически шероховатыми. В третьем случае, являющемся промежуточным между двумя вышеуказанными, абсолютная высота выступов шероховатости примерно равна толщине ламинарной пленки. В этом случае трубы относятся к переходной области сопротивления. Толщина ламинарной пленки определяется по формуле:
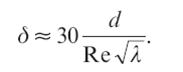
(1)
Итак, различают стенки (трубы, русла) гидравлически гладкие и шероховатые. Такое разделение является условным, поскольку, как следует из формулы (1), толщина ламинарной пленки обратно пропорциональна числу Рейнольдса (или средней скорости). Таким образом, при движении вдоль одной и той же поверхности с неизменной высотой выступа шероховатости в зависимости от средней скорости (числа Рейнольдса) толщина ламинарной пленки может изменяться. При увеличении числа Рейнольдса толщина ламинарной пленки δ уменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины ламинарной пленки и шероховатость станет влиять на характер движения и, следовательно, на потери напора.
Для последующих практических расчетов можно принимать ориентировочные значения высоты выступа шероховатости для труб: трубы новые стальные и чугунные - Δ ≈ 0,45 - 0,50 мм, трубы, бывшие в эксплуатации (так называемые «нормальные»), Δ ≈ 1,35 мм.
Таким образом, зная высоту выступа шероховатости и определив толщину ламинарной пленки, можно, сравнив их размеры, определить, гидравлически гладкой или гидравлически шероховатой будет стенка, ограничивающая поток в трубе.
Вопрос № 40.Опыты Никарудзе. Основные линии и области (зоны) сопротивления на графике зависимости коэффициента сопротивления трения от числа Рейнольдса при разных значениях относительной шероховатости.
При исследовании вопроса об определении коэффициента потерь напора на трение в гидравлически гладких трубах можно прийти к мнению, что этот коэффициент целиком зависит от числа Рей-нольдса. Известны эмпирические формулы для определения коэффициента трения, наиболее широкое распространение получила формула Блазиуса:

По данным многочисленных экспериментов формула Блазиуса подтверждается в пределах значений числа Рейнольдса от 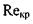 до 1-10 5.
до 1-10 5.
И. И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределенная зернистая шероховатость.
Первая область — область малых Rе и /г0, где коэффициент от шероховатости не зависит, а определяется лишь числом Rе; это область гидравлически гладких труб. Она не имеет места для максимальных значений шероховатости в опытах И. И. Никурадзе.
Во второй области коэффициент т зависит одновременно от двух параметров — числа Rе и относительной шероховатости.
Третья область — область больших Rе и /г0, где коэффициент не зависит от Rе, а определяется лишь относительной шероховатостью. Эту область называют областью автомодельности или режимом квадратичного сопротивления, так как независимость коэффициента т от Ве означает, что потеря напора пропорциональна скорости во второй степени
Чтобы лучше уяснить эти особенности сопротивления шероховатых труб, необходимо учесть наличие ламинарного слоя
Как указывалось выше, при увеличении Ве толщина ламинарного слоя л уменьшается, поэтому для турбулентного потока при малых Rе толщина ламинарного слоя больше высоты бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения Rе толщина л уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на сопротивление. При больших Rе толщина ламинарного слоя становится весьма малой, а бугорки шероховатости обтекаются турбулентным потоком с вихре-образованиями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, характерный для данной области.
График И. И. Никурадзе позволяет построить примерную зависимость от Ве допустимой шероховатости, т. е. такого максимального значения, при котором шероховатость трубы еще не влияет на ее сопротивление. Для этого следует взять те точки на графике (см. рис.), в которых кривые для шероховатых труб начинают отклоняться от прямой В для гладких труб. Очевидно, что с увеличением Rе значение допустимой шероховатости уменьшается.
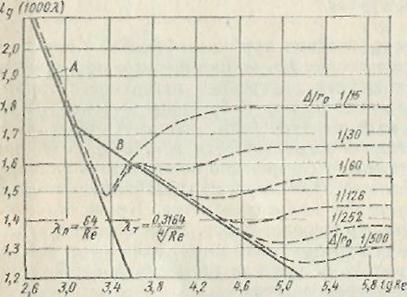
I ламинарное течение жидкости (прямая А), 
II турбулентное течение жидкости в гидравлически гладких трубах (прямая В),
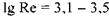
III переходная область течения жидкости, 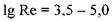
IV квадратичная область течения жидкости, 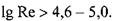
Дата добавления: 2015-04-18; просмотров: 1732; Мы поможем в написании вашей работы!; Нарушение авторских прав |