Типовые потери напора в местных сопротивлениях

в– колено без закруглений; 1 – колено; 2 – тройник; 3 – вентиль

Наиболее характерный случай -внезапное расширение жидкости, когда площадь живого сечения резко увеличивается от S1 до S2. При этом наблюдается следующее: частицы жидкости, пройдя живое сечение 1–1 с некоторой скоростью, стремятся двигаться дальше с той же скоростью. Однако они задерживаются частицами, находящимися впереди, обладающими меньшими скоростями ввиду увеличившегося живого сечения 2–2. Вследствие этого перед живым сечением 2–2 в углах образуется кольцевое пространство А, заполненное жидкостью, не участвующей в общем потоке. Так как на граничной поверхности действуют силы внутреннего трения, то эта жидкость находится во вращательном, вихревом движении.

Аналогичное явление будет наблюдаться и при движении жидкости в колене, где также образуются вихревые зоны. На образование вихрей, естественно, тратится некоторая доля энергии. Эти потери напора в местных сопротивлениях, называемые местными потерями, определяются по формуле (11.7), в которой коэффициент А заменяется коэффициентом x

hм= xv2/2g,(11.7)

где x– коэффициент местного сопротивления; v – скорость жидкости за местным сопротивлением.

Коэффициент xобычно определяется экспериментально.

Потери напора особенно ощутимы, если трубопроводы составлены из коротких участков часто изменяющих направление, имеющих изгибы, насыщенных различными местными сопротивлениями. Такие трубопроводы особенно распространены в маслопроводах двигателей и гидросистем трансмиссий автомобилей, ВГМ, тракторов, самолетов, а также в водопроводных системах жилых зданий, промышленных предприятий.

Вопрос №56. Какова особенность расчета трубопровода с последовательным, параллельным соединением труб, сифонного, разветвленного и сложного трубопроводов?
Простой трубопровод – если он не имеет ответвлений. Они могут быть соединены между собой и образуют последовательное, параллельное соединения и разветвление трубопроводов.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода меньше чем в конце. Эта разность энергий создается:

1. работой насоса

2. благодаря разности уровней жидкостей

3. давлением газов
Пусть простой трубопровод расположен произвольно. Имеет общую длину Lдиаметр dи содержит ряд местных сопротивлений.
В сечении 1-1 геометрическая высота = Z₁ , а в сечении 2-2 Z₂
Скорость потока одинакова и 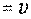. Уравнение Бернулли для сечений 1-1 и 2-2, при 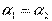и исключении скоростных напоров имеет вид:
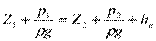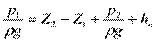; (1)
Пьезометрическую высоту 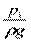называют потребным напором
если она задана, то она называется располагаемым напором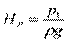
Обозначим 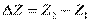, тогда 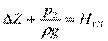– статический напор
Слагаемое 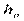представляем, как степенную функцию расхода .
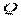Последовательное соединение трубопроводов
Возьмем несколько трубопроводов различных 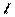и различных содержащих различные местные сопротивления и соединим их последовательно.

При подаче жидкости по такому трубопроводу будет один и тот же, а полная потеря напора между М и N равна сумме потерь во всех трубах.
(1)
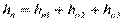(2)
Эти уравнения определяют правила постарения напорных характеристик последовательно соединенных трубопроводов.
Чтобы построить эту напорную характеристику, следует в соответствии с уравнением (2) сложить потери при одинаковых расходах, т.е. сложить ординаты всех трех кривых напорных характеристик при одинаковых абсциссах.
Параллельное соединение трубопроводов.
Это такое соединение трубопроводов 1, 2, 3 между М и N :

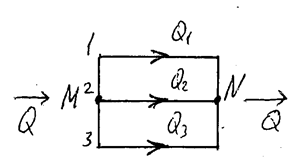
Обозначим полные напоры в М и N как 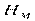и 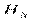. Для простоты допускаем, что трубы расположены в горизонтальной плоскости. Расход в основной магистрали ;
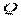Расход в параллельных трубопроводах ;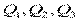
Суммарные потери напора в этих трубопроводах .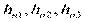
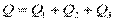(1)
Потери напора в трубопроводах:
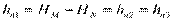(2)
Потери напора в параллельных трубопроводах равны между собой. В общем случае потери:

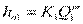
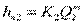(3)

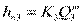
Следовательно, 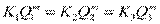(4)
Система уравнений (1) (4) позволяет решать разные задачи расчета параллельных трубопроводов. Например, задан расход в основной магистрали Q и размеры трубопроводов, а необходимо найти расходы в параллельных трубопроводах Q₁ , Q₂ , Q₃ . Пользуясь уравнениями (1) и (4) можно составить столько уравнений, сколько параллельных трубопроводов между точками М и N.
Из уравнений (1) и (2) следует :
для построения напорной характеристики параллельного соединения трубопроводов следует сложить абсциссы (расходы)