Средняя величина в статистике, ее сущность и условия применения. Виды и формы средних.

Средние величины – это обобщающие показатели общественных явлений по одному количественно варьирующему признаку. Ср. выражает типичное единиц совокупности. Особенности ср.: 1) она характеризует ту или иную совокупность в целом; 2) в ней ср. погашаются отдельные индивидуальные отклонения единиц по изучаемому признаку; 3) ср. отражает типичные черты и свойства массы единиц; 4) в сочетании с методом статистических группировок возникает возможность изучения взаимосвязей между группировочными и результативными признаками; 5) ср. величина является базой для прогнозирования; 6) многие процессы изучаются только на основании ср.; 7) ср. показывает количественное различие и сходство двух совокупностей. При расчете ср.: 1) расчет только однородных по качеству совокупностей, для этого надо сочетать метод ср. и метод группировок2) общее ср. необходимо дополнять групповыми средними и индивидуальными величинами3) для расчета ср. нужна масса единиц4)необходимо правильно выбирать единицу совокупности ср.В каждом конкретном случае применяется одна из ср. величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Все они - класс степенных средних и объединяются общей формулой (при различных значениях m): . Различают следующие виды степенных средних: 1)m = -1 – гармоническая ; 2)m = 0 – геометрическая ; 3)m = 1 – арифметическая ; 4) m = 2 – квадратическая ; 5) m = 3 – ср. кубическая . Ср. арифметическая: наиболее распространенный вид средних. Ср. арифметическая применяется в форме простой ср. и взвешенной ср. Ср. арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений. Ср. арифметическая взвешенная – ср. сгруппированных величин х₁,х₂,…,х_п – вычисляется по формуле: . В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (% или доли единиц). Тогда формула ср. арифметической взвешенной будет иметь вид: , где - частость, т.е. доля каждой частоты в общей сумме всех частот. Если частоты подсчитываются в долях (коэффициентах), то и формула средней арифметической взвешенной имеет вид: 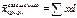. Ср. гармоническая: когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение , применяется формула ср. гармонической взвешенной:.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется ср. гармоническая простая. Ср. геометрическая: применяется, когда характеризуют средний коэффициент роста.Она исчисляется извлечением корня степени п из произведения отдельных значений. Широко применяется для определения средних темпов изменения в рядах динамики, а также в рядах распределения. Ср. квадратическая: применяется, когда нужен расчет среднего размера признака, выраженного в квадратных единицах измерения. Она бывает простой, средней, кубической, кубической (простой, взвешенной). Особым видом средних величин являются структурные ср. К таким показателям относятся мода и медиана. Мода М_о – значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. Модальный интервал определяется по наибольшей частоте. Медиана М_е – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные части – меньше медианы и больше медианы. Необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В случае четного объема ряда медиана равна средней из двух вариантов. Значение медианы вычисляется линейной интерполяцией по формуле: .