
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о вариации признака в совокупности. Система показателей вариации.Ее применение в анализе финансово-экономической деятельности предприятия.
Вариация-различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. К показателям вариации относятся:размах вариации,среднее линейное отклонение,дисперсия,среднее квадратическое отклонение, коэффициент вариации.размах вариации R,  .Размах вариации показывает лишь крайние отклонения признака. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Это среднее линейное отклонение
.Размах вариации показывает лишь крайние отклонения признака. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Это среднее линейное отклонение 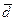 (среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической). Среднее линейное отклонение для несгруппированных данных:
(среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической). Среднее линейное отклонение для несгруппированных данных: 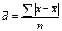 , где п – число членов ряда; для сгруппированных данных:
, где п – число членов ряда; для сгруппированных данных:  , где
, где 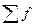 - сумма частот вариационного ряда. Дисперсияпризнака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий. Простая дисперсия для несгруппированных данных:
- сумма частот вариационного ряда. Дисперсияпризнака - средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий. Простая дисперсия для несгруппированных данных:  ; взвешенная дисперсия для вариационного ряда:
; взвешенная дисперсия для вариационного ряда: 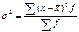 . Cвойства дисперсии: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, дисперсия не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия уменьшится или увеличится в
. Cвойства дисперсии: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, дисперсия не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия уменьшится или увеличится в  раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:  , где i – величина интервала;
, где i – величина интервала; 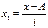 -новые (преобразованные) значения вариантов (А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
-новые (преобразованные) значения вариантов (А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);  - момент второго порядка;
- момент второго порядка;  - квадрат момента первого порядка. Среднее квадратическое отклонение
- квадрат момента первого порядка. Среднее квадратическое отклонение  равно корню квадратному из дисперсии: для несгруппированных данных:
равно корню квадратному из дисперсии: для несгруппированных данных:  , для вариационного ряда:
, для вариационного ряда:  . Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Исчисляем среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака
. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Исчисляем среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака  . Дисперсия альтернативного признака:
. Дисперсия альтернативного признака:  . Подставив в формулу дисперсии q = 1 – p, получим
. Подставив в формулу дисперсии q = 1 – p, получим  . Таким образом,
. Таким образом,  - дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака
- дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака  . Для сравнения вариаций различных признаков, используют относительный показатель вариации – коэффициент вариации. Коэффициент вариации отношение среднего квадратического отклонения к средней арифметической:
. Для сравнения вариаций различных признаков, используют относительный показатель вариации – коэффициент вариации. Коэффициент вариации отношение среднего квадратического отклонения к средней арифметической:  . Также коэффициент вариации используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%
. Также коэффициент вариации используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%
Дата добавления: 2015-04-18; просмотров: 362; Мы поможем в написании вашей работы!; Нарушение авторских прав |