Вопрос 9. Вопрос 10 Цвет — качественная субъективная характеристика электромагнитного излучения оптического диапазона

Вопрос 10 Цвет — качественная субъективная характеристика электромагнитного излучения оптического диапазона, определяемая на основании возникающего физиологического зрительного ощущения, и зависящая от ряда физических, физиологических и психологических факторов.

Каждый цвет обладает количественно измеряемыми физическими характеристиками (спектральный состав, яркость): яркость

Одинаково насыщенные оттенки, относимые к одному и тому же цвету спектра, могут отличаться друг от друга степенью яркости. К примеру, при уменьшении яркости синий цвет постепенно приближается к чёрному.

Любой цвет при максимальном снижении яркости становится чёрным.

Следует отметить, что яркость, как и прочие цветовые характеристики реального окрашенного объекта, значительно зависят от субъективных причин, обусловленных психологией восприятия. Так, к примеру синий цвет при соседстве с жёлтым кажется более ярким. (Brightness, иногда ее обозначают Lightness).

Цветовой тон (оттенок — Hue) характеризует положение данного цвета на цветовом круге. Красный цвет принят за нулевое значение, положение остальных цветов характеризуется величиной угла между данным тоном и красным. Для чистых спектральных цветов достаточно этого параметра. Однако цвет может быть осветлен (уменьшена его насыщенность) или затемнен (уменьшена яркость).

Насыщенность (Saturation — Sat) характеризует монохроматичность цвета. Для чистых спектральных цветов его величина максимальна. Чем меньше насыщенность, тем светлее цвет. При нулевой насыщенности чистый спектральный цвет становится белым.

Яркость (Brightness — Light) имеет максимальное значение для чистых спектральных цветов. При снижении яркости цвет становится темным. При нулевой яркости любой цвет превращается в черный.

насыщенность — это интенсивность определенного тона, то есть степень визуального отличия хроматического цвета от равного по светлоте ахроматического (серого) цвета. Насыщенный цвет можно назвать сочным, глубоким, менее насыщенный — приглушенным, приближенным к серому. Полностью ненасыщенный цвет будет оттенком серого. Насыщенность — одна из координат цвета в пространстве HSV. В физическом плане насыщенность цвета определяется характером распределения излучения в спектре видимого света. Наиболее насыщенный цвет образуется при существовании пика излучения на одной длине волны, в то время как более равномерное по спектру излучение будет восприниматься как менее насыщенный цвет. В субтрактивной модели формирования цвета, например при смешении красок на бумаге, снижение насыщенности будет наблюдаться при добавлении белых, серых, черных красок, а также при добавлении краски дополнительного цвета. Два оттенка одного тона могут различаться степенью блёклости. Например, при уменьшении насыщенности синий цвет приближается к серому.

Цветовой тон Тон — одна из трех основных характеристик цвета наряду с насыщенностью и светлотой. Тон определяется характером распределения излучения в спектре видимого света, причем, главным образом, положением пика излучения, а не его интенсивностью и характером распределения излучения в других областях спектра. Именно тон определяет название цвета, например «красный», «синий», «зеленый». любой хроматический цвет может быть отнесён к какому-либо определённому спектральному цвету. Оттенки, сходные с одним и тем же цветом спектра (но различающиеся, например, насыщенностью и яркостью), принадлежат к одному и тому же тону. При изменении тона, к примеру, синего цвета в зеленую сторону спектра он сменяется голубым, в обратную — фиолетовым.

Вопрос 11 Цвет аддитивный и субтрактивный

Аддитивный цвет получается при соединении света разных цветов. В этой схеме отсутствие всех цветов представляет собой чёрный цвет, а присутствие всех цветов - белый. Схема аддитивных цветов работает с излучаемым светом, например, монитор компьютера. В схеме субтрактивных цветов происходит обратный процесс. Здесь получается какой-либо цвет при вычитании других цветов из общего луча света. В этой схеме белый цвет появляется в результате отсутствия всех цветов, тогда как их присутствие даёт чёрный цвет. Схема субтрактивных цветов работает с отражённым светом.

Система цветов RGB

Монитор компьютера создает цвет непосредственно излучением света и, использует схему цветов RGB. Если с близкого расстояния посмотреть на экран монитора, то можно заметить, что он состоит из мельчайших точек красного, зелёного и синего цветов. Компьютер может управлять количеством света, излучаемого через любую окрашенную точку и, комбинируя различные сочетания любых цветов, может создать любой цвет. Будучи определена природой компьютерных мониторов, схема RGB является самой популярной и распространённой, но у неё есть недостаток: компьютерные рисунки не всегда должны присутствовать только на мониторе, иногда их приходится распечатывать, тогда необходимо использовать другую систему цветов - CMYK.

Система цветов CMYK

Данная система была широко известна задолго до того, как компьютеры стали использоваться для создания графических изображений. Для разделения цветов изображения на цвета CMYK применяют компьютеры, а для полиграфии разработаны их специальные модели. Преобразование цветов из системы RGB в систему CMYK сталкивается с рядом проблем. Основная сложность заключается в том, что в разных системах цвета могут меняться. У этих систем различна сама природа получения цветов и то, что мы видим на экране мониторов никогда нельзя точно повторить при печати. В настоящее время существуют программы, которые позволяет работать непосредственно в цветах CMYK. Программы векторной графики уже надёжно обладают этой способностью, а программы растровой графики лишь в последнее время стали предоставлять пользователям средства работы с цветами CMYK и точного управления тем, как рисунок будет выглядеть при печати.

Системы цветов HSB и HSL

Системы цветов HSB и HSL базируется на ограничениях, накладываемых аппаратным обеспечением. В системе HSB описание цвета представляется в виде тона, насыщенности и яркости. В другой системе HSL задаётся тон, насыщенность и освещённость. Тон представляет собой конкретный оттенок цвета. Насыщенность цвета характеризует его относительную интенсивность или частоту. Яркость или освещённость показывают величину чёрного оттенка добавленного к цвету, что делает его более тёмным. Система HSB хорошо согласовывается с моделью восприятия цвета человеком, то есть он является эквивалентом длины волны света. Насыщенность - интенсивность волны, а яркость - общее количество света. Недостатком этой системы является то, что для работы на мониторах компьютера её необходимо преобразовать в систему RGB, а для четырехцветной печати в систему CMYK.

Вопрос 12 Цветовая палитра

Существует несколько методов представления цвета на экране монитора. Два основных из них используются инструментами Animation Shop. Это модели RGB и HSB. Цветовая модель RGB (Red, Green, Blue) представляет собой сочетание в различных пропорциях трех основных цветов — красного (Red), зеленого (Green), синего (Blue). При наложении одного компонента основного цвета на другой яркость суммарного излучения увеличивается. Совмещение трех компонентов дает ахроматический серый цвет, который при увеличении яркости приближается к белому цвету. При 256 градационных уровнях тона черному цвету соответствуют нулевые значения RGB, а белому — максимальные значения (255, 255,255). Цветовая модель HSB (HSL) разработана с максимальным учетом особенностей восприятия цвета человеком. Она описывается тремя компонентами: оттенком (Hue), насыщенностью (Saturation) и яркостью

Электронная цветовая палитра по предназначению подобна палитре художника, но включает гораздо большее число цветов .Электронная палитра состоит из определенного числа ячеек, каждая из которых содержит отдельный цветовой тон. Конкретная цветовая палитра соотносится с определенной цветовой моделью, так как ее цвета созданы на основе цветового пространства этой модели. Но если в цветовой модели можно воспроизвести любой из описываемых ею цветов, то цветовая палитра содержит ограниченный набор цветов, называемых стандартными.

Глубина цвета - количество памяти (в битах) для воспроизведения определенной палитры цветов. Глубина́ цве́та (ка́чество цветопереда́чи, би́тность изображе́ния) — это термин компьютерной графики, означающий количество бит, используемых для представления цвета при кодировании одного пикселя растровой графики или видео framebuffer-а[1]. Это понятие также известно, как bits per pixel (bpp) задающее точное количество используемых бит для представления цвета.

Цветоделе́ние — разделение исходного изображения на цветовые составляющие, каждая из которых содержит только одномерный (численный) уровень — цветовые плоскости.

Цветовые модели

Наиболее распространенной моделью субстрактивного синтеза цвета является полиграфическая система CMYK — голубой, пурпурный, жёлтый, ключевой (чёрный). Помимо субстрактивной схемы, в теории цветовоспроизведения выделяют аддитивную. Она предполагает не вычитание цветовых составляющих из «белого» потока, а суммирование разноцветных потоков в единый результирующий поток. Одним из вариантов аддитивной схемы является модель RGB — красный, зелёный, синий). Если субстрактивная схема применяется в полиграфии (с «нулём» в белой бумаге), то аддитивная (обладающая бо́льшим цветовым охватом) — в телевизорах, мониторах и т.п., где выключенный экран выглядит чёрным.

Цветоделение в полиграфии

Цветоделение в современной полиграфии — процесс подготовки цветных изображений к печати несколькими красками. Данная технология использует принцип субстрактивного синтеза цвета, предполагающий, что на материал, отражающий или пропускающий свет (например, бумагу или прозрачную пленку) наносятся слои цветных красителей, каждый из которых «вычитает» из белого цвета свою долю спектра.

Вопрос 13 Кривой линией называется траектория точки, перемещающейся в пространстве по какому-либо закону. Однако, имеются кривые линии, не описываемые какой-либо закономерностью (незакономерные кривые линии). Кривая линия может быть также определена как однопараметрическое множество точек. Плоской кривой линией называется линия, каждая точка которой принадлежит одной плоскости. В противном случае кривая линия называется пространственной (винтовая линия, линии пересечения двух поверхностей, из которых хотя бы одна является кривой поверхностью).

Кривые линии могут быть образованы движением точки в пространстве, пересечением кривой поверхности плоскостью (кривые Персея), взаимным пересечением двух поверхностей. Кривые Персея, например, образуются при пересечения торовых поверхностей плоскостью.

На рисунке 8.2 представлены некоторые алгебраические кривые линии второго, третьего и четвертого порядков, а также трансцендентные кривые линии.

Наиболее часто в технике применяются лекальные кривые линии, которые могут быть плоскими и пространственными. К ним относятся эллипс, парабола, гипербола, эвольвента, циклоида, винтовая линия и другие, примеры которых приведены на рисунке 8.3. Способы построения лекальных кривых обычно рассматривается в курсе технического черчения.

Эвольвента – траектория точки касательной, перекатываемой без скольжения по окружности. Иногда её неправильно называют разверткой окружности.

Синусоида – кривая линия, описываемая уравнением y = sin x.

Гипербола – геометрическое место точек, разность расстояний которых от двух точек, называемых фокусами, есть величина постоянная.

Винтовая линия – траектория точки, перемещающейся по образующей цилиндра, конуса или тора, в то время как сама образующая равномерно вращается вокруг оси упомянутых поверхностей.

Эллипс – геометрическое место точек, сумма расстояний которых до двух точек, называемых фокусами, есть величина постоянная.

Парабола – геометрическое место точек, равноудаленных от некоторой точки, называемой фокусом, и некоторой прямой, называемой директрисой.

Циклоида – траектория точки окружности, перекатываемой без скольжения по прямой линии. При построении эпи- и гипоциклоиды окружность перекатывают по окружности.

Особыми точками называются точки, в которых можно провести не одну, а две и более касательных или в которых изменяется направление движения точки или вращения касательной.

На эпюре кривые линии задаются множеством точек, принадлежащих линии (рисунок 8.5). Возможны табличный и аналитический способы задания.

Вопрос 14 Кривая Безье — параметрическая кривая, задаваемая выражением

где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.

, где n — степень полинома, i — порядковый номер опорной вершины

Виды кривых Безье

[править] Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:

.

[править] Квадратные кривые

Квадратная кривая Безье (n = 2) задаётся 3-я опорными точками: P0, P1 и P2.

.

Квадратные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах.

[править] Кубические кривые

В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

.

Кубическая кривая Безье

Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.

В современных графических системах, таких как PostScript, Metafont и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.

Применение в компьютерной графике

Благодаря простоте задания и возможности удобно манипулировать формой, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Поскольку кривая полностью определяется своей выпуклой оболочкой из опорных точек, последние могут быть отображены и использоваться для наглядного управления формой линии. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также легко могут быть осуществлены путём применения трансформаций к опорным точкам. Наличие выпуклой оболочки значительно облегчает задачу о точках пересечения кривых Безье: если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые.

Наибольшее значение имеют кубические кривые Безье. Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Вопрос 15При использовании машинной графики можно по желанию изменять масштаб изображения, вращать его, смещать и трансформировать для улучшения наглядности перспективного изображения. Для начала заметим, что точки на плоскости задаются с помощью двух ее координат. Таким образом, геометрически каждая точка задается значениями координат вектора относительно выбранной системы координат. Координаты точек можно рассматривать как элементы матрицы [x,y], т. е. в виде вектор-строки или вектор-столбца. Положением этих точек управляют путем преобразования матрицы.

Точки на плоскости xy можно перенести в новые позиции путем добавления к координатам этих точек констант переноса:

.

Таким образом, для перемещения точки на плоскости надо к матрице ее координат прибавить матрицу коэффициентов преобразования.

Рассмотрим результаты матричного умножения матрицы [x,y], определяющей точку Р, и матрицы преобразований 2´2 общего вида: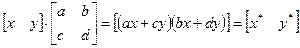

Отображение В то время как чистое двумерное вращение в плоскости xy осуществляется вокруг оси, перпендикулярной к этой плоскости, отображение определяется поворотом на 180° вокруг оси, лежащей в плоскости ху. Такое вращение вокруг линии у = х происходит при использовании матрицы

.Преобразованные новые выражения определяются соотношением

Вращение вокруг у = 0 получается при использовании матрицы

Если подвергнуть общему преобразованию различные геометрические фигуры, то можно установить, что параллельные прямые преобразуются в параллельные прямые, середина отрезка – в середину отрезка, параллелограмм – в параллелограмм, точка пересечения двух линий – в точку пересечения преобразованной пары линий.