Полезности. Законы Госсена.

Полезность – способность блага удовлетворять потребности. Это общее и совершенно бесспор­ное положение не дает нам почти ничего для понимания поведения поку­пателя на рынке, если мы не рассмотрим некоторые закономерности само­го процесса потребления.

Для более точного описания процесса убывания полезности в экономи­ческой науке используется понятие предельной полез­ности, т. е. добавочной полезности, прибавляемой каждой последней пор­цией товара. Используя это понятие, сфор­мулируем закон убывающей предельной полезности: по мере увеличения количества потребляемого товара его предельная полезность имеет тенден­цию к сокращению. Этот закон обычно называют первым законом Госсена.

При удовлетворении потребностей человек начинает с самой неотложной потребности, а затем постепенно переходит к менее неотложным, действуя таким образом, что, в конце кон­цов, предельные полезности употребляемых благ станут одинаковы. Таким образом, можно сформулировать второй закон Госсена: при максимизации общей полезности предельная полезность всех потребляемых благ должна быть одной и той же величины. Но человек, приобретая блага на рынке, тратит разные суммы денег, поскольку у каждого товара своя рыночная цена. Если мы разделим пре­дельную полезность блага на его цену, то получим взвешенную предельную полезность. Учитывая это, каждый потребитель расширяет отдельные виды потребления до тех пор, пока предельные полезности не оказываются про­порциональны ценам, или пока не оказываются одинаковыми взвешенные предельные полезности. Проще говоря, последний рубль, затраченный, на­пример, на мясо, должен представлять ту же полезность, что и последний рубль, затраченный на хлеб или апельсины. Это условие равновесия потребителя может быть выражено следую­щим образом:

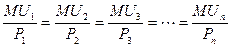
где MU - предельная полезность отдельных товаров, а Р - их цена.

Кардиналисты были заняты поиском измерителя абсолютных величин предельной полезности (У.Джевонс, А.Маршалл, Д.Робертсон и др.). Однако эти поис­ки не увенчались успехом и чаще всего при сравнении использовались де­нежные оценки полезности.

6. Ординалистский подход к анализу полезности: аксиомы, кривая безразличия, бюджетная линия, оптимум потребителя

Кривая безразличия.

В.Парето высказал идею о том, что вместо абсо­лютных измерений предельной полезности плодотворнее было бы перейти к анализу относительному, а именно: определить предпочтение одних ком­бинаций товаров покупателей (потребителей) другим комбинациям, или наборам товаров. Инструментом такого анализа явились так называемые кривые безразличия, которые широко используются неоклассической школой при исследовании многих микроэкономических процессов, связан­ных с проблемой выбора. Свойства кривой безразличия: 1. имеет отрицательный наклон и вогнута к началу координат; 2. множество кривых безразличий в одной системе координат называется «картой кривых безразличий»; 3. кривые безразличия никогда не пересекаются, т.е. они параллельны; 4. предпочтительнее та кривая безразличия, которая лежит выше и правее.

Итак, обратимся к проблеме оптимизации потребления с точки зрения ординалистского подхода. Равновесие потребителя может быть показано графически с помощью вышеназванных кривых безразличия. Возьмем потребителя, располагающе­го фиксированным денежным доходом, который он целиком тратит на по­требление. Для простоты предположим, что он покупает только два вида товаров: А и В. Очевидно, что имеются некоторые комбинации количества этих товаров, которые дают равную общую полезность для потребителя (на­пример, два товара А и три товара В имеют такую же общую полезность, как три товара А и два товара В и т. д.). Отказ от одного из товаров компенсиру­ется получением другого товара в большем количестве. К этим комбинаци­ям товаров А и В потребитель, следовательно, в равной мере безразличен. Если эти комбинации покажем гра­фически, то получим плавную кривую безразличия U₂ (рис. ниже).