Оптимальные методы обнаружения сигналов с полностью известными параметрами

Пусть сигнал зависит от параметра а, который может находиться в состояниях a₁ и a₀ с вероятностями p₁ и p₀ соответственно, причем p₁ + p₀ = 1, поскольку возможны только эти два состояния параметра а. Случайный процесс X (t) на входе приемного устройства имеет сигнальную составляющую s (t) и аддитивную помеху :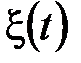

.

Возможный вид реализации x (t) представлен на рис.1.

Рис.1

Произведем дискретизацию полученной выборки по времени. Дискретные значения в моменты времени t_i обозначим соответственно для сигнала, помехи и суммы сигнала и помехи:

; ; .

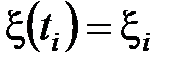Интервал дискретизации Dt равен интервалу корреляции помехи, т.е. 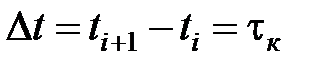, тогда выборки помехи будут некоррелированными. Если помеха распределена по нормальному закону

,

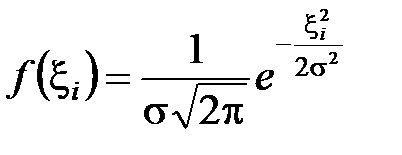где s² - дисперсия помехи, то во время приема сигнала с помехой единичные измерения будут иметь следующие плотности вероятности:

; .

Для нормальных процессов некоррелированность равнозначна независимости, и тогда совместное распределение n измерений в выборке X будет равно произведению одномерных плотностей вероятности единичных измерений:

. (1)

Аналогично для параметра а₁

. (2)

Апостериорная плотность вероятности для параметра а может быть определена по формулам

;

.

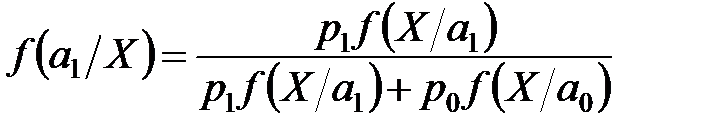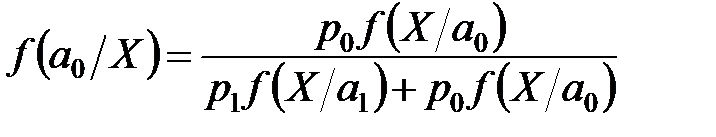В соответствии с принципом максимума правдоподобия решающее правило может быть записано так:

,

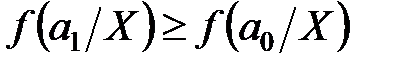и тогда выносится решение, что d = d₁, или

,

где - отношение правдоподобия.

Решение о том, что d = d₁, выносится, если 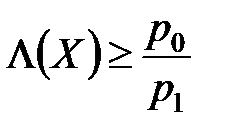, а решение d = d₀, если . Для нормального процесса отношение правдоподобия определим, используя формулы (1) и (2):

. (3)

Поскольку монотонное преобразование не смещает положение максимума функции, то в выражении (3) прологарифмируем обе его части, и тогда правило решения примет вид

=

.

Положим p₁ = p₀ (задача вязи), тогда

.

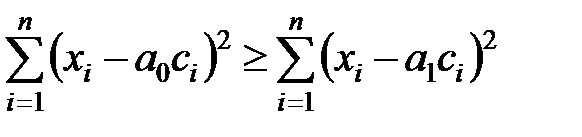Умножив обе части неравенства на Dt и совершив предельный переход при Dt ® 0 и n ® ¥, суммы в выражении примут вид интегралов, и правило обнаружения сигнала может быть приведено к такому виду:

.

Если a₁ = 1, a₀ = 0, что соответствует задаче обнаружения сигнала на фоне шума, то последнее выражение упростится:

,

где Е - энергия сигнала, равная .

В левой части последнего неравенства - корреляционный интеграл, который соответствует проекции вектора сигнала на вектор суммы помехи и сигнала в многомерном пространстве. Эта проекция сравнивается с пороговой величиной. Полученное правило решения является оптимальным, т.е. наилучшим в рассматриваемой ситуации. Синтез полученной процедуры приводит к взаимокорреляционному приемнику (рис.2).

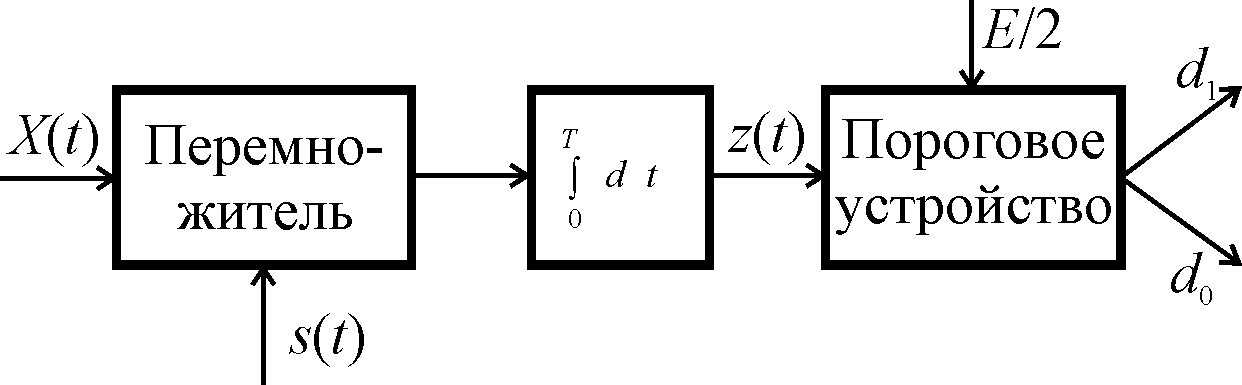
Рис.2

Билет №4

4.1