Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где 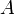— амплитуда колебаний маятника, — начальная фаза колебаний, 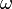— циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями

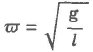
№19 Уравнение гармонических колебаний для физического маятника.

Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).

Рис.1

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы

где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, F_τ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления F_τ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение запишем как
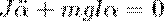или
Принимая
получим уравнение

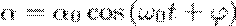
Из формулы вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом

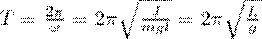
где введена величина L=J/(ml) — приведенная длина физического маятника.

№20 Закон равного распределения энергии по степеням свободы в термодинамике.

Большинство химических веществ состоит из многоатомных молекул. Если рассматривать газообразное состояние вещества, то при столкновениях молекул тепловая энергия газа случайным образом расходуется на изменение кинетических энергий поступательного и вращательного движений молекул, а также на возбуждение колебаний атомов в молекуле. Естественно предположить, что указанные движения в молекуле могут происходить одновременно.

Средняя энергия приходящаяся на одну степень свободы: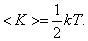

У одноатомной молекулы i = 3, тогда для одноатомных молекул

для двухатомных молекул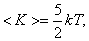

для трёхатомных молекул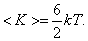

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

Если система находится в состоянии термодинамического равновесия, при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы. На каждую поступательную i_п и вращательную i_вр степени свободы приходится энергия 1/2 kT. Для колебательной i_кол, степени свободы она равна kT. Таким образом число степеней свободы i = i_п + i_вр + 2i_кол
Закон о равномерном распределении энергии по степеням свободы перестает быть справедливым при квантовом описании системы частиц, когда каждому квантовому состоянию системы с i-степенями свободы соответствует ячейка объемом hⁱ в фазовом пространстве “координаты – импульсы” тождественных (неразличимых между собой) частиц, где h – постоянная Планка (М. Планк (1858-1947) – немецкий физик–теоретик).