Работа. Кинетическая энергия частицы.

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

и/или

Механическая энергия бывает двух видов: кинетическая и потенциальная. Кинетическая энергия (или энергия движения) определяется массами и скоростями рассматриваемых тел. Потенциальная энергия (или энергия положения) зависит от взаимного расположения (от конфигурации) взаимодействующих друг с другом тел.

Работа определяется как скалярное произведение векторов силы и перемещения. Скалярным произведением двух векторов называется скаляр равный произведению модулей этих векторов и косинус угла между ними.

Понятия энергии и работы тесно связаны друг с другом.

Кинетическая энергия частицы

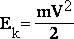
доп.

работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы.

№10Момент импульса тела, вращающегося вокруг неподвижной оси.

Момент импульса материальной точки относительно точки O определяется векторным произведением
, где 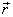— радиус-вектор, проведенный из точки O, — импульс материальной точки.
Момент импульса материальной точки относительно неподвижной оси равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим
.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
.

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
.

№11 Момент импульса системы. Закон сохранения момента импульса.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

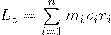
Используя формулу v_i = ωr_i, получим

т. е. 2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство

(3)

В замкнутой системе момент внешних сил и откуда

(4)

Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).

№12 Момент импульса и момент силы относительно точки и оси. Уравнение моментов.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Рис.1

Модуль вектора момента импульса

где α - угол между векторами r и р, l - плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен
(1)
и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

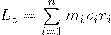
Используя формулу v_i = ωr_i, получим
т. е. 2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Момент силы. Момент силы относительно точки .
Момент силы относительно неподвижной оси равен проекции вектора на эту ось.
Проекция вектора на ось не зависит от положения точки, относительно которой определяется радиус-вектор силы .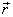
Если вектор лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.

Определение моментов сил: , .

№13 Момент инерции твердого тела.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

§ m_i — масса i-й точки,

§ r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела вовращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

где:

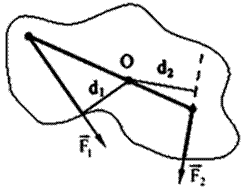
§ — масса малого элемента объёма тела ,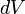

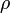§ — плотность,

§ — расстояние от элемента 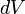до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

№14 Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси.

Момент силы. Момент силы относительно точки .
Момент силы относительно неподвижной оси равен проекции вектора на эту ось.
Проекция вектора на ось не зависит от положения точки, относительно которой определяется радиус-вектор силы .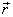
Если вектор лежит в плоскости перпендикулярной оси вращения, то проекция момента силы на ось равна произведению величины силы на плечо. Плечо силы — это длина перпендикуляра, опущенного на прямую, вдоль которой направлена сила.

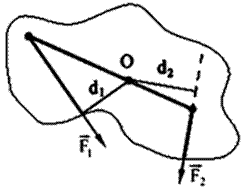
Определение моментов сил: , .

Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси:
суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение:
.
Учитывая, что момент импульса твердого тела , уравнение динамики твердого тела можно представить в виде
.

№15 Момент инерции. Теорема Штейнера.

Момент инерции. Твердое тело можно представить в виде системы жестко связанных между собой материальных точек.
Момент инерции системы материальных точек относительно оси вращения равен сумме произведений масс материальных точек системы на квадраты их расстояний до оси вращения:
.

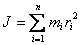где:

§ m_i — масса i-й точки,

§ r_i — расстояние от i-й точки до оси.

Для расчета момента инерции используют интегрирование:
.

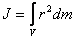Единица измерения СИ: кг·м².