Вычисление пройденного пути. Средние значения

При малых ∆t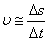

Весь путь s, пройденный точкой, можно представить как сумму путей: ∆s₁, ∆s₂, …, ∆s_N пройденных за соответствующие промежутки времени ∆t;

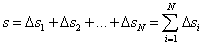
каждое из слагаемых ∆s_і (і — любое число от 1 до N) может быть приближенно представлено в виде

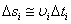
где ∆t_і — промежуток времени, за который был пройден ∆s_і, a v_i — одно из значений скорости за время ∆t_і. Таким образом,

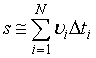
В пределе при стремлении всех ∆t_і к нулю (количество промежутков ∆t_і будет при этом неограниченно возрастать) сумма, стоящая справа, станет точно равна s:

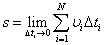
Величину пройденного пути можно представить как площадь фигуры, которая ограничена кривой зависимости величины скорости v от времени t. График функции v=v(t) (рис. 22).

Движение, при котором скорость, изменяясь как угодно по направлению, остается постоянной по величине, называется равномерным.

При равномерном движении все υ_і в формуле будут одинаковы и равны v.

Сумма элементарных промежутков времени дает время t, за которое точка проходит путь s.

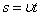
при равномерном движении скорость равна пути s деленному на время t за которое он пройден:

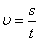
Скорость при равномерном движении равна по величине пути, проходимому движущейся точкой за единицу времени.