Закон Ома для однородного проводника. Закон Ома в дифференциальной форме.

Немецкий физик Г. Ом (1787—1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению Uна концах проводника:

(1) гдеR— электрическое сопротивление проводника. Уравнение (1) выражает закон Ома для участкацепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула (1) позволяет установить единицу сопротивления — ом (Ом) 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина G=1/R называется электрической проводимостью проводника. Единица проводимости — сименс(См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника противление Rпрямо пропорционально его длине lи обратно пропорционально площади его поперечного сечения S: 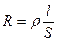(2)где — коэффициент пропорциональности, характеризующий материал проводниканазываемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом-метр (Ом·м).

Закон Ома можно представить в дифференциальной форме.

Подставив выражение для сопротивления (2) в закон Ома (1), получим 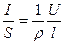(3)где

величина, обратная удельному сопротивлению, называется удельной электрической проводимостью вещества проводника. Ее единицасименс на метр (См/м). Учитывая, что — напряженность электрического в проводнике, I/S=j— плотность тока, формулу (3) можно записать в виде 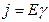Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу можно записать в виде 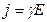. Это выражение — закон Ома в дифференциальнойформе, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

26. Циркуляция вектора . Потенциал.

Электростатическое поле является потенциальным: работа кулоновских сил по перемещению заряда не зависит от формы траектории последнего ,а определяется только положением начальной и конечной точек. Если перемещать заряд по замкнутой траектории ,то работа полем не совершается.

Циркуляция вектора напряженности электростатического поля вдоль (замкнутого) контура L также равна нулю :

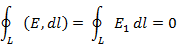
Где dl- элемент контура L,по направлению совпадающий с направлением обхода контура; Е1- проекция вектора Е на направление dl

Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:

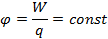
- энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.

…

- следствие принципа суперпозиции полей (потенциалы складываются алгебраически).

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.