Поток вектора напряженности электростатического поля. Теорема Гаусса. Интегральная и дифференциальная формы.

Поток вектора напряженности электростатического поля.

Электростатическое поле наглядно можно изобразить с помощью силовых линий (линий напряженности). Силовыми линиями называют кривые, касательные к которым в каждой точке совпадают с вектором напряженности Е.

Силовые линии являются условным понятием и реально не существуют. Силовые линии одиночного отрицательного и одиночного положительного зарядов 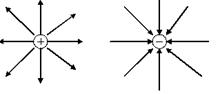Рис.5

Если густота и направление силовых линий по всему объему поля сохраняются неизменными, такое электростатическое поле считается однородным. Например, заряд, распределенный равномерно по бесконечной плоскости, создает однородное электрическое поле, силовые линии которого изображаются равноотстоящими друг от друга параллельными прямыми линиями. Для того, чтобы силовые линии характеризовали не только направление поля, но и значение его напряженности, число линий должно быть численно равно напряженности поля Е.

Число силовых линий dФ_Е, пронизывающих площадку dS, перпендикулярную к ним, определяет поток вектора напряженности электростатического поля:

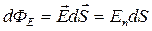где E_n= Еcos α-проекция вектора Е на направление нормали n к площадке dS.

Соответственно поток вектора Е сквозь произвольную замкнутую поверхность S

Теорема Гаусса

Зная дивергенцию вектора а в каждой точке пространства, можно вычислить поток этого вектора через любую замкнутую поверхность конечных размеров.

Сделаем это сначала для потока вектора v (потока жидкости). Произведение divv на dVдает мощность источников жидкости, заключенных в объеме dV. Сумма таких произведений, т. е. , дает сум­марную алгебраическую мощность источников, заключенных в объе­ме V, по которому осуществляется интегрирование. Вследствие несжимаемости жидкости суммарная мощность источников должна равняться потоку жидкости, вытекающему наружу через поверх­ность S, ограничивающую объем V. Таким образом, мы приходим к соотношению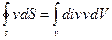

Аналогичное соотношение выполняется для векторного поля любой природы:

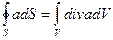
Это соотношение носит название теоремыОстроград­ского — Гаусса. Интеграл в левой части соотношения вычи­сляется по произвольной замкнутой поверхности S, интеграл в правой части — по объему V, ограниченному этой поверхностью.

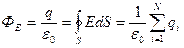Теорема Гаусса: Эта теорема гласит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .