Магнитное поле кругового проводника с током

Исследования показали, что линии магнитной индукции поля кругового тока не являются правильными окружностями, но они замыкаются, обходя проводник, по которому идет ток. Направление линий магнитной индукции можно определить с помощью правила правого винта (правило буравчика): если головку винта вращать в направлении тока в проводнике, то поступательное движение острия винта покажет направление магнитной индукции в центре кругового тока.

В центре кругового тока модуль магнитной индукции может быть вычислен по формуле

I

где R — радиус кругового проводника.

36. Теорема о потоке вектора .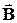

Подобно тому, как было введено понятие потока вектора напряженности электрического поля, введем понятие потока вектора магнитной индукции, или магнитного потока. Элементарный магнитный поток через малую элементарную площадку , которую можно считать плоской, и в окрестности которой магнитное поле можно считать однородным, равен произведению вектора индукции на площадь выделенного элемента поверхности и косинус угла между вектором индукции и нормалью к поверхности: .

Поток может быть как положительным, так и отрицательным в зависимости от направления нормали к поверхности.

За единицу магнитного потока в системе единиц СИ принят вебер (Вб). 1 Вб – это магнитный поток через поверхность площадью 1 м2 , расположенную в однородном магнитном поле перпендикулярно вектору индукции β,

В случае неоднородного магнитного поля поток через какую-либо поверхность равен алгебраической сумме потоков через участки поверхности, вблизи которых поле можно считать однородным.

Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами.

37. Теорема о циркуляции вектора .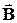

Теперь обратимся к циркуляции вектора . По определению интеграл по замкнутому контуру L вида называется циркуляцией вектора индукции магнитного поля.Проще всего вычислить этот интеграл в случае поля прямого тока. Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис. 24.3, а), ток перпендикулярен к плоскости чертежа и направлен за чертеж) В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку. Заменим в выражении для циркуляции через 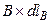( – проекция элемента контура на направление вектора ). Из рисунка видно, что равно b da, где b – расстояние от провода с током до dl, da – угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок .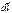

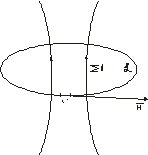
Таким образом, подставив выражение (23.12) дляВ, получим:

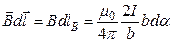. (24.6)

С учетом равенства (3.6) имеем:

. (24.7)

При обходе по контуру, охватывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому 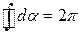. Иначе обстоит дело, если ток не охватывается контуром (рис. 24.3, б). В этом случае при обходе по контуру радиальная прямая поворачивается сначала в одном направлении (участок 1-2), а затем в противоположном (участок 2-1), вследствие чего равен нулю. Учтя этот результат, можно написать: , (24.8)

где под I следует подразумевать ток, охватываемый контуром. Если контур тока не охватывает, циркуляция вектора равна нулю.

Из (24.8) можно сделать следующие выводы:

1) магнитное поле прямолинейного тока – вихревое, так как в нем циркуляция вектора вдоль линии магнитной индукции не равна нулю;

2) циркуляция вектора поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на величину силы тока.

Знак выражения (24.8) зависит от направления обхода по контуру (в этом же направлении отсчитывается угол ). Если направление обхода образует с направлением тока правовинтовую систему, величина (24.8) положительна, в противном случае – отрицательна. Знак можно учесть, полагая I алгебраической величиной, причем положительным нужно считать ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления будет отрицательным

С помощью соотношения (24.8) легко восстановить в памяти формулу (23.12) для В поля прямого тока. Представим себе плоский контур в виде окружности радиуса b (рис. 24.4).

В каждой точке этого контура вектор одинаков по величине и направлен по касательной к окружности.

Следовательно, циркуляция равна произведениюВ на длину окружности 2 , и соотношение (24.8) имеет вид

.

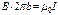Отсюда (ср. с (23.12)).

Циркуляцией вектора 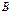по заданному замкнутому контуру называется интеграл

,

где 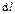- вектор элементарной длины контура, направленной вдоль обхода контура, - составляющая вектора в направлении касательной к контуру, - угол между векторами и .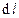

Закон полного тока: циркуляция вектора по замкнутому контуру 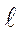равна алгебраической сумме токов, охватываемых этим контуром:

Данный закон справедлив для постоянного магнитного поля.

38.Магнитное поле в веществе. Токи намагничивания. Теорема о циркуляции вектора намагниченности .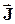

Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.

Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетикиидиамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).

Рисунок 1.19.1. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле.

Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против индукции внешнего поля.

В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.

39 Напряженность магнитного поля . Теорема о циркуляции .