СОПРОТИВЛЕНИЕ И ПРОВОДИМОСТЬ ПРОВОДНИКОВ. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ ОТ ФИЗИЧЕСКИХ УСЛОВИЙ

При замыкании электрической цепи, на зажимах которой име­ется разность потенциалов, возникает электрический ток. Свобод­ные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении свободные электроны натал­киваются на атомы проводника и отдают им запас своей кинетиче­ской энергии.

Таким образом, электроны, проходя по проводнику, встречают сопротивление своему движению. При прохождении элект­рического тока через проводник последний нагревается.

Электрическим сопротивлением проводника (оно обозначается латинской буквой r) обусловлено явление преобразования электри­ческой энергии в тепловую при прохождении электрического тока по проводнику. На схемах электрическое сопротивление обозна­чается так, как показано на рис. 18.

За единицу сопротивления принят 1 ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому, вместо того чтобы писать: «Сопротивление проводника равно 15 ом», можно написать просто: r = 15 Ω.

1000 ом называется 1 к и л о о м (1 ком, или 1 к Ω).

1 000 000 ом называется 1 м е г о м (1 мгом, или 1 MΩ).

Прибор, обладающий переменным электрическим сопротивле­нием и служащий для изменения тока в цепи, называется реоста­том. На схемах реостаты обозна­чаются, как показано на рис. 18. Как правило, реостат изготовляется из проволоки того или иного сопро­тивления, намотанной на изолирую­щем основании. Ползунок или рычаг реостата ставится в определенное по­ложение, в результате чего в цепь вводится нужное сопротивление.

Длинный проводник малого по­перечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.

Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.

Температура проводника тоже оказывает влияние на его сопро­тивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, константан', никелин и др.) с увеличением температуры своего со­противления почти не меняют.

Итак, мы видим, что электрическое сопротивление проводника зависит от длины проводника, поперечного сечения проводника, ма­териала проводника, температуры проводника.

При сравнении сопротивлений проводников из различных ма­териалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.

Сопротивление (в омах) проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозна­чается греческой буквой ρ (ро).

Сопротивление проводника можно определить по формуле

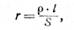
где r — сопротивление проводника, ом;

ρ — удельное сопротивление проводника;

l — длина проводника, м;

S — сечение проводника, мм2.

Из указанной формулы получаем размерность для удельного со­противления

В табл. 1 даны удельные сопротивления некоторых проводников.

Из таблицы видно, что железная проволока длиной 1 м и сече­нием 1 мм2 обладает сопротивлением 0,13 ом. Чтобы получить 1 ом сопротивления, нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро — 1 ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро — лучший проводник, но большая стоимость се­ребра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм" обладает сопротивлением 0,0175 ом. Чтобы получить сопротивление в 1 ом, нужно взять 57 м такой проволоки.

Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготов­ления проводов, кабелей, обмоток электрических машин и аппара­тов. Широко применяют также в качестве проводников алюминий и железо.

Подробная характеристика металлов и сплавов приведена в табл. 2.

Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм²:

Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сече­нием 2,5 мм2:

Из формулы сопротивления легко можно определить длину, удельное со­противление и сечение проводника.

Пример3. Для радиоприемника необходимо намотать сопротивление в 30 ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки:

Пример 4. Определить сечение нихромовой проволоки длиной 20 Ж, если сопротивление ее равно 25 ом:

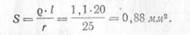
Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивле­ние 16 ом. Определить материал проволоки.

Материал проводника характеризует его удельное сопротивление

По таблице удельных сопротивлений находим, что таким со­противлением обладает свинец.

Ранее было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включен амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут умень­шаться. Это показывает, что с нагревом сопротивление металли­ческой проволоки увеличивается.

У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40—50%. Имеются сплавы, которые незначи­тельно меняют свое сопротивление с нагревом. Некоторые спе­циальные сплавы практически не меняют сопротивления при из­менении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление элек­тролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.

Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротив­ления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.

Изменение сопротивления проводника при его нагревании, при­ходящееся на 1 ом первоначального сопротивления и на 1⁰ темпера­туры, называется температурным коэффициен­том сопротивления и обозначается буквой α (альфа).

Если при температуре t₀ сопротивление проводника равно r₀, а при температуре t равно r_t, то температурный коэффициент сопро­тивления

Примечание. Расчет по этой формуле можно производить лишь в опре­деленном интервале температур (примерно до 200° С).

В табл. 3 приводим значения температурного коэффициента со­противления а для некоторых металлов.

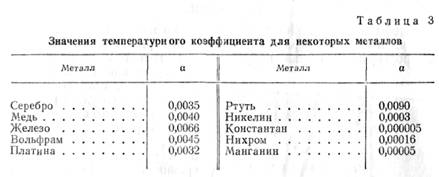
Из формулы для температурного коэффициента сопротивления определим r_t

:

Пример 6. Определить сопротивление железной проволоки, нагретой до 200°,

если сопротивление ее при 0° было 100 ом:

Пример 7. Термометр сопротивления, изготовленный из платиновой прово­локи, в помещении с температурой 15° имел сопротивление 20 ом. Термометр поме­стили в печь и через некоторое время было измерено его сопротивление. Оно ока­залось равным 29,6 ом. Определить температуру печи:

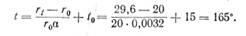
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и наоборот. Поэтому сопротивление и проводимость проводника являются обратными величинами.

Если сопротивление проводника обозначается буквой r, то про­водимость определяется как . Обычно проводимость обозначается буквой g.

Электрическая проводимость измеряется в 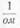(или в сименсах).

Пример 8. Сопротивление проводника равно 20 ом. Определить его проводимость.

Если r = 20 ом, то

Пример 9. Проводимость проводника равна 0,1 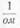. Определить его сопро­тивление.

Если , то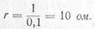

17 вопрос

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением r, которое называется внутренним со-

противлением этого источника. Таким образом, источник тока имеет две важных характери-

стики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной E, и внутренним сопротивлением r подключён к рези-

стору R (который в данном случае называется внешним резистором, или внешней нагрузкой,

или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

R

a b

E; r

Рис. 2. Полная цепь

Наша задача — найти силу тока I в цепи и напряжение U на резисторе R.

За время t по цепи проходит заряд q = It. Согласно формуле (1) источник тока совершает

при этом работу:

Aст = Eq = EIt: (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, кото-

рая выделяется на сопротивлениях R и r. Данное количество теплоты определяется законом

Джоуля–Ленца:

Q = I

2Rt + I

rt = I

(R + r)t: (3)

2Итак, Aст = Q, и мы приравниваем правые части формул (2) и (3):

EIt = I

(R + r)t:

После сокращения на It получаем:

E = I(R + r):

Вот мы и нашли ток в цепи:

I =

E

R + r

: (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0),

то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток

короткого замыкания:

Iкз =

E

r

:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма боль-

шим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе R с помощью

закона Ома для участка цепи:

U = IR =

ER

R + r

: (5)

Это напряжение является разностью потенциалов между точками a и b (рис. 2). Потенциал

точки a равен потенциалу положительной клеммы источника; потенциал точки b равен потен-

циалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на

клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет U < E — ведь E умножается на дробь,

меньшую единицы. Но есть два случая, когда U = E.

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивле-

нием. При r = 0 формула (5) даёт U = E.

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В

этом случае можно считать, что внешнее сопротивление бесконечно велико: R = 1. Тогда

величина R + r неотличима от R, и формула (5) снова даёт нам U = E.

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, под-

соединённый к полюсам источника, покажет его ЭДС.