Формальное определение концептуальной модели вычислительных процессов (КМ ВП).

В основе КМ ВП лежит понятие "процесс". Эквивалентом термина "процесс" может служить также "действие", "задача", "формулировка задачи" и т.д. Но смысл, объединяющий эти понятия, остается постоянным: это некоторое преобразование (отображение) подмножества данных, называемых входными по отношению к рассматриваемому процессу, в другое подмножество данных, именуемое выходными. Выполнение данного преобразования соответствует переводу системы из одного состояния в некоторое другое.

Вычислительный процесс рассматривается как формулировка задачи, решение которой возможно в данной ПрО. Другими словами, процесс есть работа, производимая последовательным процессором при выполнении программы с ее данными.

Таким образом, вычислительный процесс есть совокупность действия и объектов (данных) необходимых для его реализации и формируемых в результате выполнения.

Информационные объекты, используемые при решении задач, не могут возникнуть из ничего. Они порождаются процессами и являются результатами их выполнения.

Построение КМВП соответствует переходу от неформальных знаний о функционировании ПрО к формальному описанию вычислительных процессов на определенном языке, допускающем единственную интерпретацию.

Концептуальность модели заключается в том, что в ней описываются в первую очередь состав, структура и отношения между информационными объектами (далее просто объектами) и процессами независимо от конкретного способа их реализации при написании программ на языке программирования.

В качестве теоретической основы математической модели языка применяется аксиоматическая теория множеств.

КМ ВП включает:

множества процессов и объектов модели;

отношения, задаваемые над множествами элементов модели;

множества атрибутов элементов модели;

множества функциональных отношений между информационными объектами, процессами и их атрибутами.

Первые два компонента образуют схему вычислительного процесса, а последние – модель атрибутов.

Схема вычислительного процесса (S_ВП) определяется следующим кортежем множеств:

,

где P={p_i} –множество процессов обработки информации;

O={o_i} – множество информационных объектов ;

H={H_p, H_o} – отношения иерархии:

– отношения иерархии процессов;

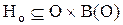– отношения иерархии инфообъектов;

Q = {In, Out} – отношения взаимодействия;

– отношения входные инфообъекты процесса процесс;

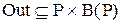– отношения процесс – выходные инфообъекты процесса;

– отношения следования процессов.

Каждый из перечисленных в схеме компонентов имеет свою семантическую интерпретацию.

Описываемые в S_ВП отношения (H, Q, S) устанавливаются между некоторым процессом (объектом) и некоторым подмножеством множеств P и O (элементом B(P), B(O), где B - булеан).

Булеаном множества D (B(D)) называется множество всех допустимых подмножеств (включая D и "пустое" Æ) множества D.

Пример: D={1, 2, 3}. B(D)={{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},Æ}

|B(D)|=2ⁿ, где n = |D|.

Отношения иерархии H_p, H_oустанавливают соответствие между отдельными процессами (объектами) и множествами подчиненных им процессов (объектов). Отношения иерархии удобно представлять в форме функциональных отображений:

где p_i – суперпроцесс;

{p_j} – множество подчиненных p_i процессов;

o_i – информационный суперобъект;

{o_j} – множество подчиненных o_i объектов.

Запись вида: 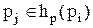говорит о том, что процесс p_j принадлежит множеству процессов, подчиненных процессу p_i.

Аналогично для .

Отношения взаимодействия Q позволяют определить входные и выходные инфообъекты процессов:

где {o_i} – совокупность входных, а {o_j} – совокупность выходных инфообъектов процесса p_i.

Каждой тройке <входные объекты процесса, процесс, выходные объекты процесса> может быть поставлено в соответствие предложение следующего вида:

которое рассматривается как:

аксиома вычислимости для процессов самого нижнего уровня иерархии ;

теорема вычислимости для процессов промежуточных уровней иерархии , существование доказательства которой, является одним из условий корректности модели, проверяемых в ходе анализа разрешимости модели вычислительного процесса.

Отношения следования S задают частичный порядок выполнения процессов:

,

где {p_i} – множество процессов, которые обязательно должны быть выполнены перед запуском процесса