Аксиомы ZFC

1. Аксиома объёмности. Два множества a и b равны тогда и только тогда, когда они имеют одни и те же элементы.

2. Аксиома пустого множества. Существует множество e без единого элемента. Это множество обычно обозначается {} или .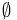

3. Аксиома пары. Для любых множеств a и b существует множество c такое, что a и b являются его единственными элементами. Множество c обозначается {a,b} и называется неупорядоченной парой a и b. Если a = b, то c состоит из одного элемента.

4. Аксиома объединения. Для любого семейства a множеств существует множество , называемое объединением множества a, состоящее из тех и только тех элементов, которые содержатся в элементах множества a.

5. Аксиома бесконечности. Аксиомы с 1 по 4 предоставляют ограниченные возможности для формирования новых множеств. Так, по теореме Кантора во множестве 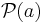имеется элемент, не принадлежащий a, поэтому, например, не существует «множества всех множеств» (парадокс Рассела). Далее введём определение: множество называется индуктивным, если оно а) содержит пустое множество и б) содержит последователь (то есть элемент ) каждого своего элемента. Аксиома бесконечности утверждает, что индуктивные множества существуют.

6. Схема выделения. Любому множеству a и свойству отвечает множество b, элементами которого являются те и только те элементы a, которые обладают свойством . Схема выделения содержит счётное количество аксиом, так как каждая формула логики первого порядка порождает аксиому.

7. Аксиома множества подмножеств. Для любого множества a существует множество b, состоящее из тех и только тех элементов, которые являются подмножествами множества a. Множество подмножеств множества a обозначается .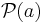

8. Схема подстановки. Пусть - такая формула, что при любом x₀ из множества X существует, и притом единственный, объект y₀ такой, что выражение истинно. Тогда объекты c, для каждого из которых существует d из X такой, что истинно, образуют множество. Схема подстановки содержит счётное количество аксиом, так как каждая подходящая формула порождает аксиому.

9. Аксиома основания. Каждое непустое множество s содержит элемент a такой, что .

10. Аксиома выбора. Для каждого семейства A непустых непересекающихся множеств существует множество B, имеющее один и только один общий элемент с каждым их множеств X, принадлежащих A.

Вопрос2

1.Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики) от n переменных — в дискретной математике отображение Bⁿ → B, где B = {0,1} — булево множество.

2. Суперпозицией булевых функций f₀ и f₁,...,f_n называется функция f(x₁,...,x_m) = f₀(g₁(x₁,...,x_m),...,g_k(x₁,...,x_m)), где каждая из функций g_i(x₁, ...,x_m) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f₁,...,f_n.

3. Существенные и фиктивные переменные

существенная переменная булевой функции , если найдется такой набор переменных , что

Переменная, которая не является существенной для булевой функции, называется фиктивной переменной.

Задание 3

Обсуждали на 3 лабе

Билет 3

Вопрос 1

1. Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.

Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:

Числа, заданные таким образом, называются ординальными.

Первые несколько ординальных чисел и соответствующие им натуральные числа:

2. Аксиомы Пеано: Множество будем называть множеством натуральных чисел, если зафиксирован некоторый элемент (единица) и функция (функция следования) так, что выполнены следующие условия

1. (1 является натуральным числом);
2. Если , то (Число, следующее за натуральным, также является натуральным);
3. (1 не следует ни за каким натуральным числом);
4. Если S(b) = a и S(c) = a, тогда b = c (если натуральное число a непосредственно следует как за числом b, так и за числом c, то b = c);
5. Аксиома индукции. Пусть P(n) — некоторый одноместный предикат, зависящий от параметра — натурального числа n. Тогда:

если P(1) и , то

Вопрос2.

1.Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

· V это непустое множество вершин

· A это множество (упорядоченных) пар различных вершин, называемых ориентированными рёбрами(ребро со стрелкой показыаещее куда можно пройти)

.Неориентированный графне содержит ориентированные ребра (нет стрелочек показывающих направления)

2.Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).

3. Суграф (частичный граф) исходного графа — граф, содержащий все вершины исходного графа и подмножество его рёбер.

4. Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром

5.Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.

Билет4

Вопрос1

1. Прямым произведением¹⁾, или декартовым произведением²⁾ множеств и называется множество всех упорядоченных пар таких, что и . При этом используют следующее обозначение:
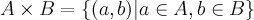
2. Упорядоченная n-ка называетсяеще n-мерным упорядоченным набором, вектором, точкой, кортежем
3. Отношение - это одна из форм всеобщей взаимосвязи всех предметов, явлений, процессов в природе, обществе и мышлении.( бинарные отношение представляется множеством упорядоченных пар элементов)

Обычно отношения обозначают латинской буквой R.

Если хRх для любого х из поля отношения R то такое отношение называют рефлексивным

Если хRу ® уRх, то такое отношение называется симметричным

Если (xRy Ùy R z) ® xRz, то такое отношение называется транзитивным

Одновременное выполнение трех отношение есть отнашения эквиволентности

4. Пусть даны два множества Х и У и каждому элементу х О Х поставлен в соответствие единственный элемент у О У, который обозначен через f(х). В этом случае говорят, что на множестве Х задана функция f и пишут:f : Х ® У.

5. Отображение называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X

Отображение называется инъекцией (или вложением, или отображением в Y), если разные элементы множества X переводятся в разные элементы множества Y.

Биекция одновременное выполнение инъекции и сюръекции.

Вопрос 2- на лабе делала.

Билет5

Вопрос1

1. Композицией (произведением, суперпозицией) бинарных отношений и 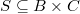называется такое отношение 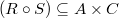, что:
2. Инверсия(Обратное отношение) R — это множество 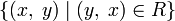и обозначается, как R ^{− 1}.
3. операции

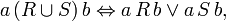
• R(ST) = (RS)T,
• (RS) ^{− 1} = S ^{− 1}R ^{− 1},
• ,
• ,
• ,
• ,
• 

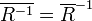4. Бинарные отношения могут обладать различными свойствами, такими как

• Рефлексивность: .
• Антирефлексивность (иррефлексивность): .
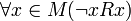• Симметричность: .
• Антисимметричность: .
• Транзитивность: .
• Асимметричность: . Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Вопрос 2

1. Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу
2. Эйлеров цикл — это эйлеров путь, являющийся циклом.
3. Теоре́ма Э́йлера в теории чисел гласит:

Если a и m взаимно просты, то , где φ(m) — функция Эйлера.

Билет 6

Вопрос 1

1. Отношение эквивалентности (∼) на множестве X — это бинарное отношение , для которого выполнены следующие условия:

1. Рефлексивность: для любого a в X,
2. Симметричность: если , то ,
3. Транзитивность: если и , то .

2.Совокупность всех классов эквивалентности называется фактор-множеством. Оно обозначается символом X/R.

3. Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств

Билет 7

Вопрос 1

1.Мощность множества, или кардинальное число множества, — это обобщение понятия количества (числа) элементов множества, которое имеет смысл для всех множеств, включая бесконечные.

Для мощностей множеств можно ввести отношение частичного порядка, поэтому одно бесконечное множество может быть больше или меньше другого. Среди бесконечных множеств счётное множество является самым маленьким.

2.В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество X является счётным, если существует биекция , где обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.

3.Несчётное множество — такое бесконечное множество, которое не является счётным. Таким образом, любое множество является либо конечным, либо счётным, либо несчётным.

Вопрос 2

1. Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом.

2. Необходимое условие:Если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины x(i) с локальной степенью p(x(i)) < 2.

Билет8

Вопрос 1

1.Множество всех подмножеств данного множестваА называется множеством – степени множества А и обозначается Р(А)={X такой что Х < А} , то есть если А ={1, 2 ,3 } то множества подмножеств Р(А) = {0(пустое множество),(1),(2),(3),(1,2),(1,3),(2,3),(1,2,3)}

2. В теории множеств теорема Кантора гласит, что

Вопрос 2

1. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

2. Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.

Билет 9

Вопрос 1

1. Мощность множества, или кардинальное число множества, — это обобщение понятия количества (числа) элементов множества, которое имеет смысл для всех множеств, включая бесконечные.

2. Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности. Класс множеств, биективно эквивалентных данному, не является, однако, множеством

3.Теорема Кантора — Бернштейна (в англ. литературе теорема Кантора — Бернштейна — Шрёдера), утверждает, что если существуют инъективные отображения и между множествами A и B, то существует взаимооднозначное отображение . Другими словами, что мощности множеств A и B совпадают:

| A | = | B | .

Другими словами, теорема утверждает следующее:

Из и следует, что где — кардинальные числа

Вопрос 2

1. Графы G₁ и G₂ наз. гомеоморфными, если существуют такие их подразбиения, к-рые изоморфны(ГРАФОВ ИЗОМОРФИЗМ

- отношение эквивалентности на множестве графов)

2. Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных , и не содержит подграфов, гомеоморфных . Необходимость

Необходимость условия очевидна.