Теорема (о пяти красках)

Каждый планарный граф можно так раскрасить, используя пять цветов, что любые две смежные вершины будут окрашены в разные цвета.

2. Гипотеза четырех красок — каждый планарный граф 4-раскрашиваем.

3. Правильная раскраска графа – это раскраска каждой его вершины в

один из К цветов таким образом, чтобы смежные вершины были раскрашены

в разные цвета

Билет 11

Вопрос 1

1.Пусть М и М*- два частично упорядоченных множества и пусть f есть отображения М в М*.

МЫ скажем что это отображение сохраняет порядок если из а<b и a,b принадлежит М следует что f(a) < f(b). Отображение F называется изоморфизмом частично упорядоченного множества М и М* ,если он биективен , и соотношение f(a)< f(b) выполняется только в том случае если а<b. Сами множества М и М* называются изоморфными между собой.

Вопрос 2

1. Плоский граф — геометрический граф, в котором никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины (не пересекаются)

2. Планарный граф — граф, который может быть изображён на плоскости без пересечения рёбер

3. Теорема Эйлера : Для связного плоского графа справедливо следующее соотношение между количеством вершин | V(G) | , ребер | E(G) | и граней | F(G) | (включая внешнюю грань):

Если каждая грань ограничена не менее чем тремя ребрами (при условии, что в графе больше двух ребер), а каждое ребро разделяет две грани, то

следовательно,

то есть, при большем числе ребер такой граф заведомо непланарен.

Билет 12

Вопрос 1

1. Элемент называется минимальным , если не существует элемента b < a. Другими словами, a — минимальный элемент, если для любого элемента либо b > a, либо b = a, либо b и a несравнимы.

2. Условие минимальности. Каждое подмножество частично упорядоченного множества обладает хотя бы одним минимальным элементом.

3. Условие обрыва убывающих цепей. Всякая строго убывающая цепь частично упорядоченного множества обрывается.

4. Условия индуктивности: посмотреть зависимость для 1 элемента потом для к-ого потом если это зависимость выполниться для к+1 элемента то условие выполнено.(хз на счет верности)

5. Вполне упорядоченное множество — линейно упорядоченное множество M такое, что в любом его непустом подмножестве есть минимальный элемент, другими словами это фундированное множество с линейным порядком.

Вопрос 2

1. Точка сочленения графа 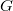- вершина, при удалении которой в 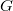увеличивается число компонент связности

2. Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

3. Числом связанности называется наименьше количество вершин, удаление которых приводит к не связанности графа или одновершинному графу .

Билет 13

Вопрос 1

1. Аксиомой выбора называется следующее высказывание теории множеств: «Для каждого семейства непустых непересекающихся множеств существует (по меньшей мере одно) множество d, которое имеет только один общий элемент c c каждым из множеств b данного

2. семейства».