
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
К эквиолентным относиться
§ Теорема Цермел
§ Принцип максимума Хаусдорфа
§ Лемма Куратовского-Цорна
Вопрос 2
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Билет 14
Вопрос 1
1. Определение. Множество А, вместе с одной или несколькими алгебраическими операциями, определенными на этом множестве называют алгебраической структурой.
2. Гомоморфизм — это морфизм в категории алгебраических систем. Это отображение алгебраической системы А, сохраняющее основные операции и основные соотношения.
3. Изоморфи́зм —В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Вопрос 2
1. Цикломатическое число графа — минимальное число ребер, которые надо удалить, чтобы граф стал ациклическим.
2. Рассмотрим каркас 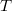 графа
графа 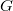 .
.  — все ребра графа
— все ребра графа 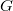 , которые не входят в каркас
, которые не входят в каркас 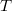 . При добавлении ei образуется простой цикл
. При добавлении ei образуется простой цикл  . Семейство циклов
. Семейство циклов  называется фундаментальными циклами графа
называется фундаментальными циклами графа 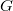 относительно каркаса
относительно каркаса 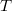
Билет 15
Вопрос 1
1. Гру́ппа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Группы являются важными инструментами в изучении симметрии во всех её проявлениях. Примерами групп являются вещественные числа с операцией сложения, множество вращени плоскости вокруг начала координат и т. п.
2. Решётка в теории множеств — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю , так и точную нижнюю грани;
3. Определение. Множество R с двумя определенными в нем алгебраическими операциями, сложением и умножением, называется кольцом, если относительно операции сложения оно является абелевой группой, а операция умножения дистрибутивна,
Вопрос 2
1. Дерево — связный граф, не содержащий циклов.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.
2. Пусть G — произвольный (n, m)-граф с k компонентами связности. Если G — не лес, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.
Билет 16
Вопрос1
1. Булево й решеткой называется дистрибутивная решетка с дополнением (с дополнением значит что решетка обладает универсальными границами О , I в которых элемент а имеет хотя бы одно дополнение х.
Вопрос 2
1. Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n(n − 1) / 2 рёбер и обозначается Kn.
2. В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G. Чтобы найти обратный граф, дополните данный граф до полного и удалите все ребра, которые уже были до этого
3. Теорема Рамсея — теорема комбинаторики, открытая Франком Рамсеем, встречающаяся в литературе в нескольких формулировках:
Пусть p, q и r — натуральные числа, причем  . Тогда существует число . Тогда существует число  , обладающее следующим свойством: если все r-элементныеподмножества N-элементного множества S произвольным образом разбиты на два непересекающихся семейства α и β, то либо существует p-элементное подмножество множества S, все r-элементные подмножества которого содержатся в α, либо существует q-элементное подмножество, все r-элементные подмножества которого содержатся в β. , обладающее следующим свойством: если все r-элементныеподмножества N-элементного множества S произвольным образом разбиты на два непересекающихся семейства α и β, то либо существует p-элементное подмножество множества S, все r-элементные подмножества которого содержатся в α, либо существует q-элементное подмножество, все r-элементные подмножества которого содержатся в β.
|
| Для любых натуральных чисел N, K любой достаточно большой полный граф, ребра которого раскрашены в N цветов, содержит одноцветный полный подграф с K вершинами. |
4. Клика — полный подграф неориентированного графа. Другими словами, клика графа есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством.
Билет 17
1. Булевым кольцом называют кольцо, в котором все элементы идемпотентны (коммутативность, наличие единицы или делителей нуля не требуется).
2. Интересной особенностью булевых колец является то, что
3. 
в частности, при  , то есть булево кольцо всегда имеет характеристику два, а также, учитывая это
, то есть булево кольцо всегда имеет характеристику два, а также, учитывая это
4. 
то есть булево кольцо всегда коммутативно.
Вопрос 2
1. Двудо́льный граф или бигра́ф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Определение


Полный двудольный граф K3,2
Неориентированный граф G = (W,E) называется двудольным, если множество его вершин можно разбить на две части  , | U | > 0, | V | > 0, так, что
, | U | > 0, | V | > 0, так, что
§ ни одна вершина в U не соединена с вершинами в U и
§ ни одна вершина в V не соединена с вершинами в V
Двудольный граф называется полным, если для каждой пары вершин  существует ребро
существует ребро  . Для
. Для
| U | = i, | V | = j
такой граф называется Ki,j
2. Граф является двудольным только тогда ,когда все просты циклы имеют четную длину.
билет 18
вопрос 1
1. Способа задания множеств: Перечислением элементов:  ,Заданием определенного свойства обьектов:
,Заданием определенного свойства обьектов:  , где P — определенное свойство обьекта а .
, где P — определенное свойство обьекта а .
2. Подмножество данного множестваЕсли каждый элемент который принадлежит множеству А, принадлежит в то же время множеству В, то множество А называется подмножество, т.е. А включается в В.
3.Характеристической функцией случайной величины Х называется функция эта функция представляет собой математическое ожидание некоторой комплексной случайной величины , являющейся функцией от случайной величины Х.
4. Равенство множествпо определению, считают два множества равными, если они состоят из одних и тех же элементов:

5. Одно элементное множество.из х 
6. Неупорядочные парых и у. 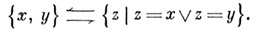
7. Множество всех подмножеств данного множестваА называется множеством – степени множества А и обозначается Р(А)={X такой что Х < А} , то есть если А ={1, 2 ,3 } то множества подмножеств Р(А) = {0(пустое множество),(1),(2),(3),(1,2),(1,3),(2,3),(1,2,3)}
Дата добавления: 2015-04-21; просмотров: 231; Мы поможем в написании вашей работы!; Нарушение авторских прав |