
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Благосостояние первого потребителя улучшится, второго ухудшится
2) благосостояние первого
потребителя ухудшится, а второго улучшится;
3) благосостояние обоих
потребителей улучшится;
4) благосостояние обоих
потребителей ухудшится; Рис.4
5) ничего определенного сказать невозможно.
Задание 19. Допустим, в экономике существуют два потребителя и два продукта: X и Y.
Функции полезности потребителей имеют следующий вид:
U1 = (x1)1/3 (y1)1/2, U2 = (x2)1/3 (y2)1/2,
где х1 и у1 - количества продуктов Х и Y, потребляемые первым потребителем,
х2 и у2 - количества продуктов Х и Y, потребляемые вторым потребителем.
Количество продуктов в экономике ограничено: Х = х1 + х2 = 60, Y = у1 + у2 = 140. Выведите уравнение контрактной линии (множество оптимальных по Парето распределений продуктов Х и Y).
*1) Y1 = (7/3)X12)Y2 = (3/7)X23) Y1 = (3/7)X14) X2 = (2/3)Y25) Y1 = (2/3)X1
Задание 20. Допустим, в экономике производится только два продукта X и Y. При производстве этих продуктов используются два производственных ресурса: капитал (К) и труд (L), количество которых ограничено. Известно, что кривая производственных возможностей (кривая продуктовой трансформации) этой экономики описывается следующим уравнением в пространстве продуктов: Х2 + Y2 = 100.
Определите предельную норму трансформации для производимых продуктов

Выберите правильный ответ:
*1)  2)
2) 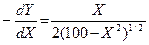 3)
3) 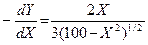
4) 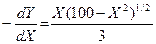 5)
5) 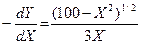
Часть 2 (25 Баллов)
Задание 1. Функция полезности индивида описывается формулой: V(С) = 100 –150/С. У индивида есть две возможности выбора:
1) получить 6 ден.ед.;
2) принять участие в лотерее, где он может выиграть 10 ден.ед. с вероятностью 1/5 или
выиграть 5 ден.ед с вероятностью 4/5.
ОПРЕДЕЛИТЕ (ответы обосновать):
 1) каково отношение индивида к риску (постройте график функции полезности Бернулли)? (2 Б) Ответ:
1) каково отношение индивида к риску (постройте график функции полезности Бернулли)? (2 Б) Ответ:
2) как оценивает индивид предельную полезность денег ? (1Б)
3) что предпочтительней для индивида: играть или получить 6 ден.ед.? Приведите аналитическое и графическое обоснования решения. (4Б)
Ответ:
6) чему равен ожидаемый выигрыш лотереи? (1Б)
Ответ:
7) чему равен безрисковый эквивалент лотереи? (2Б)
Ответ:
Задание 2. Согласно Основной теореме оптимизации потребительского выбора случайных товаров необходимое условие оптимальности потребительского набора
(С1*, С2*) формулируется следующим образом: (2Б)
Задание 3. Приведите определение относительной меры Эрроу-Пратта.
Обладает ли функция полезности V(C) = C1/4 свойством постоянности относительной меры Эрроу-Пратта. (3Б)
Ответ (обосновать):
Задание 4. Приведите определение абсолютной меры Эрроу-Пратта и пример функции полезности, имеющей постоянную абсолютную меру Эрроу-Пратта. Покажите, что для приведенной функции это свойство выполняется (4Б)
Ответ (обосновать):
Задание 5. Определите отношение к риску индивидов, чьи функции полезности описываются следующими формулами: (3Б)
Ответ (обосновать):
(а) V = ln c (б) V = c2 (в) V = 100 + 6c
Задание 6. Дано дерево игры – вариант игры «Вхождение фирмы на рынок» (F1 – фирма-новичок, F2 – фирма «старожил»).
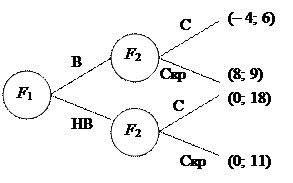 |
1) Перейти от игры в развернутой форме к игре в стратегической форме. (3Б)
Ответ:
2) Найти (с обоснованием) равновесия Нэша в чистых стратегиях игры в стратегической форме. (3Б)
Ответ:
3) Дать геометрическую интерпретацию игры в стратегической форме, используя пространство выигрышей игроков F1 и F2. (3Б)
Ответ:


4) Найти (и обосновать) Парето-эффективные пары чистых стратегий, используя геометрическую интерпретацию. (3Б)
Ответ:
Экзаменационная работа по МИКРОЭКОНОМИКЕ-2 (14 января 2009 г.)
ВАРИАНТ № 2
Часть 1 (80 Баллов)
Задание 1.Потребитель максимизирует функцию полезности:U(y1,y2)=y1y2 при заданном бюджетном ограничении. Номинальный доход равен 24. Цены базисного периода на первый и второй товары соответственно равны: p10 = 2, p20 = 4. В текущем периоде цена на первый товар повысилась и стала равной p11 = 8. Тогда величина эквивалентного изменения дохода составит: 1)-5; 2) 5; 3) -9; 4) -10; *5) -12.
Задание 2.Функция полезности потребителя U = X1X2. Потребитель максимизирует общую полезность. Начальные цены: р1 = 4, р2 = 4.
Чему равно компенсационное изменение дохода, если при снижении цены второго товара до 1 и неизменности цены первого, потребитель покупает набор: X1= 2, X2 = 8 ?
1) 16; 2) 12; 3) 8; *4) - 8; 5) – 16.
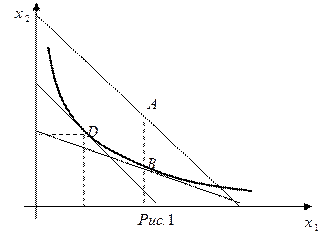 Задание 3. Известно, чтопредпочтения потребителя в пространстве двух товаровописываютсяследующей функцией полезности: U(X1, X2) = (X1)1/2 (X2)1/2, где Х1 – количество первого товара, Х2 – количество второго товара. Цена первого товара равна 2, второго – 2, доход потребителя равен 10 ден.ед. Пусть цена второго товара повысилась и стала равной 5.
Задание 3. Известно, чтопредпочтения потребителя в пространстве двух товаровописываютсяследующей функцией полезности: U(X1, X2) = (X1)1/2 (X2)1/2, где Х1 – количество первого товара, Х2 – количество второго товара. Цена первого товара равна 2, второго – 2, доход потребителя равен 10 ден.ед. Пусть цена второго товара повысилась и стала равной 5.
На рисунке 1: А – исходный набор потребителя, В – набор товаров после изменения цен, потребительские наборы B и D расположены на одной кривой безразличия.
Согласно ситуации, изображенной на рисунке 1, разность между стоимостью потребительского набора D и стоимостью набора В
1) равняется + 3,6 и называется эквивалентным изменением дохода по Хиксу;
Дата добавления: 2015-04-21; просмотров: 275; Мы поможем в написании вашей работы!; Нарушение авторских прав |