
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Адаптивное управление при априорной неопределенности (непараметрическая обработка информации).
Адаптивные системы применяются для управления объектами различной природы (и в первую очередь технологическими процессами) в условиях неопределённости.

При создании адаптивных систем управления идут двумя путями. В первом классе систем в процессе адаптации подстраивается модель объекта, а затем по модели также непрерывно по времени вычисляются управляющие воздействия. Во втором классе систем на основе критериев оптимальности синтезируется структура устройств управления, а затем в процессе адаптации подстраиваются параметры этих устройств. Жесткого различия между этими классами адаптивных систем нет. Есть области, где принципиального различия в их свойствах нет и дело, как говорится, вкуса, какой системе отдать предпочтение.
Рассмотрим объект, который находится в ряде статистических состояний. Необходимо найти такое его состояние, которое соответствует наилучшему режиму его работы. Структура системы управления представлена на рисунке. объект имеет два входа: один управляемый u, второй – наблюдаемый. Необходимо найти алгоритм работы управляющего устройства, чтобы обеспечивалось движение системы по заданной траектории  т.е. чтобы выход системы
т.е. чтобы выход системы 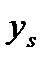 в каждый текущий дискретный момент времени
в каждый текущий дискретный момент времени  как можно меньше отличался бы от
как можно меньше отличался бы от 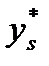 . К моменту времени
. К моменту времени 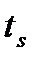 управляющее устройство располагает: измерениями выхода объекта у, контролируемого входа объекта μ, управляющими воздействиями u и желаемым выходом системы
управляющее устройство располагает: измерениями выхода объекта у, контролируемого входа объекта μ, управляющими воздействиями u и желаемым выходом системы  :
:
В момент времени 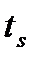 с измерительного устройства поступила свежая информация
с измерительного устройства поступила свежая информация 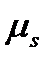 , известно также значение
, известно также значение  желаемой траектории системы и необходимо вычислить и подать на объект управляющее воздействие
желаемой траектории системы и необходимо вычислить и подать на объект управляющее воздействие 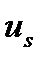 . Заметим, что только после окончания переходных процессов в объекте, вызванных воздействиями
. Заметим, что только после окончания переходных процессов в объекте, вызванных воздействиями 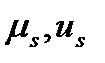 , происходит измерение выхода объекта
, происходит измерение выхода объекта  . После этого осуществляется переход к следующему такту
. После этого осуществляется переход к следующему такту 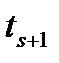 управления.
управления.
Поиск управляющего воздействия 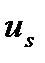 можно вести двумя путями. Первый (традиционный подход) основан на построении прямой модели объекта и последующем вычислении
можно вести двумя путями. Первый (традиционный подход) основан на построении прямой модели объекта и последующем вычислении 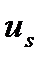 из условия наилучшего приближения выхода модели к желаемому выходу
из условия наилучшего приближения выхода модели к желаемому выходу 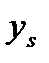 замкнутой системы. Кратко опишем этот подход, основываясь на непараметрической оценке регрессии. Все переменные объекта
замкнутой системы. Кратко опишем этот подход, основываясь на непараметрической оценке регрессии. Все переменные объекта 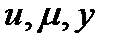 являются случайными величинами. Уравнением объекта (наилучшим по минимуму среднеквадратичного отклонения) является регрессия
являются случайными величинами. Уравнением объекта (наилучшим по минимуму среднеквадратичного отклонения) является регрессия 
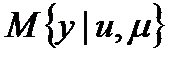 .
.
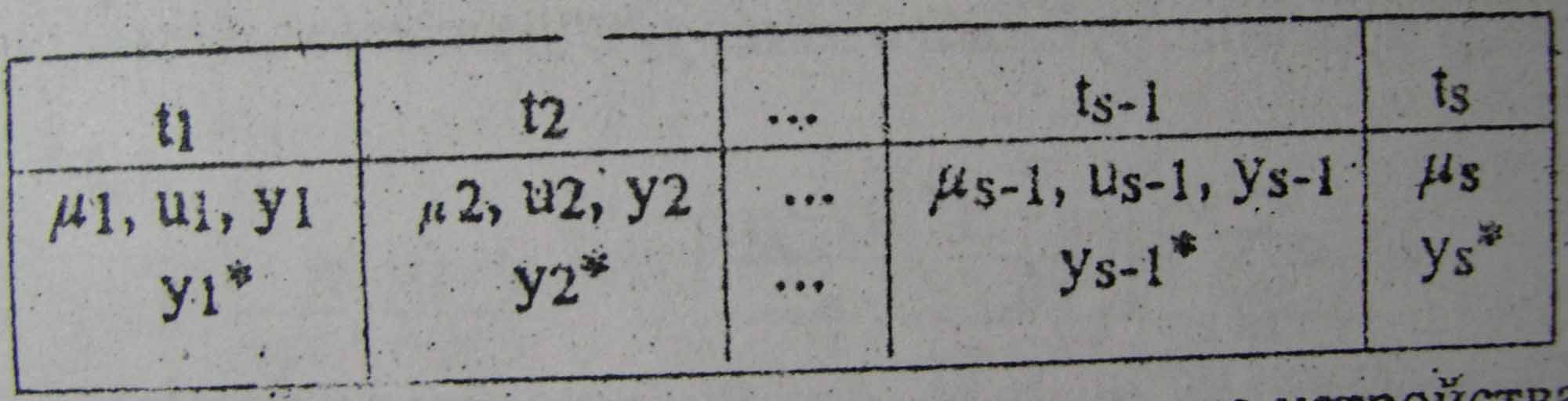
Оценив её по выборке (таблица), получаем прямую модель объекта:
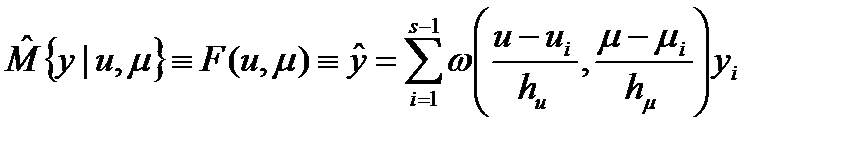 .
.
Используем её для прогноза выхода объекта в момент времени  е. Для этого подставляем вместо
е. Для этого подставляем вместо 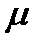 его новое измеренное значение
его новое измеренное значение 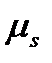 :
:
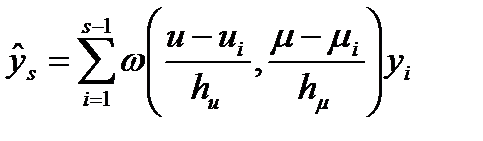
и приравниваем прогнозируемый выход 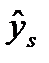 к желаемому выходу
к желаемому выходу 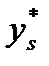 :
:
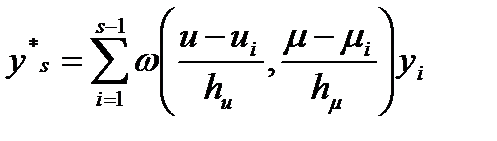 .
.
Из этого нелинейного уравнения вычисляем u и получаем искомое управляющее воздействие 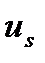 объекта в момент времени
объекта в момент времени  .
.
Если на управление u накладывается ограничение 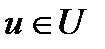 , то для поиска
, то для поиска  надо использовать критерий наилучшего приближения
надо использовать критерий наилучшего приближения  к
к 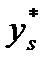 , например:
, например:
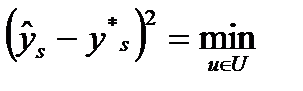 .
.
Результатом минимизации локальной (только для момента времени 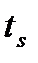 ) функции качества является искомое управление
) функции качества является искомое управление 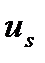 .
.
Расчёт управления является непростой обратной задачей, тем более что она решается на каждом такте  . Эта задача усложняется, если управлений несколько. чтобы избавиться от решения этой обратной задачи, воспользуемся обратным уравнением объекта. Выборка (таблица) позволяет оценить не только прямую, но и обратную регрессию:
. Эта задача усложняется, если управлений несколько. чтобы избавиться от решения этой обратной задачи, воспользуемся обратным уравнением объекта. Выборка (таблица) позволяет оценить не только прямую, но и обратную регрессию:

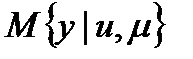 , т.е.
, т.е. 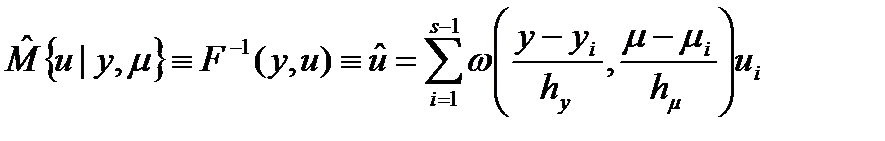 .
.
Подставляя в правую часть вместо  его новое измерение
его новое измерение 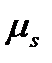 , а вместо у его желаемое значение
, а вместо у его желаемое значение 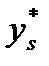 , получаем искомое управляющее воздействие:
, получаем искомое управляющее воздействие:
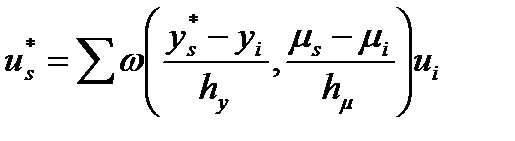 ,
,
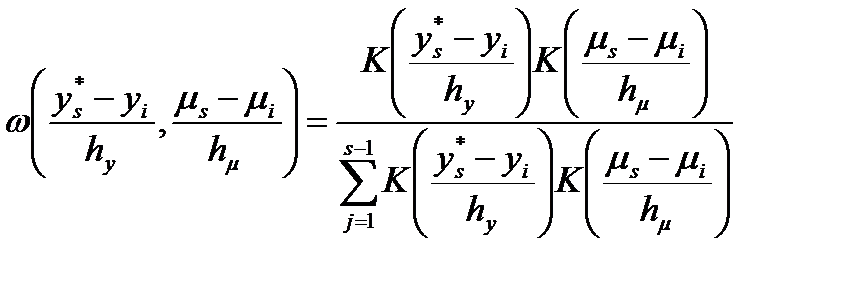 .
.
Особенностью непараметрических моделей является то, что область их действия не выходит за область экспериментов. Всегда в силу выпуклой комбинации точек 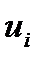 в
в 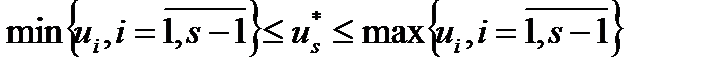 .
.
Если область наблюдений мала, а для достижения желаемого значения 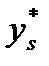 требуется управление
требуется управление 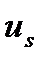 вывести из этой области, то надо к управляющему воздействию добавлять изучающую компоненту:
вывести из этой области, то надо к управляющему воздействию добавлять изучающую компоненту:
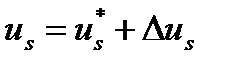 .
.
На начальном этапе управления, когда фактически идёт процесс обучения, роль изучающей добавки велика. Обычно формируют 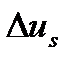 в виде некоторой функции от невязки
в виде некоторой функции от невязки  . Со временем эта невязка уменьшается и влияние изучающей добавки также падает. Аналогом изучающей добавки является задание первых значений управления на границе области её возможных значений. Остальные
. Со временем эта невязка уменьшается и влияние изучающей добавки также падает. Аналогом изучающей добавки является задание первых значений управления на границе области её возможных значений. Остальные 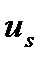 рассчитываются по формуле искомого управляющего воздействия и находятся внутри области возможных изменений управления.
рассчитываются по формуле искомого управляющего воздействия и находятся внутри области возможных изменений управления.
Изучающая добавка 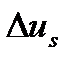 к управлению должна удовлетворять условиям
к управлению должна удовлетворять условиям

Выполнение их обеспечивает асимптотическую сходимость:
 .
.
Если внешнее возмущение  объекта отсутствует либо оно остаётся постоянным в процессе управления, то непараметрическое управление статистическим режимом работы объекта зависит только от измеряемых значений выхода объекта yi, желаемого выхода
объекта отсутствует либо оно остаётся постоянным в процессе управления, то непараметрическое управление статистическим режимом работы объекта зависит только от измеряемых значений выхода объекта yi, желаемого выхода 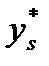 и предшествующих значений управления:
и предшествующих значений управления:
 ,
, 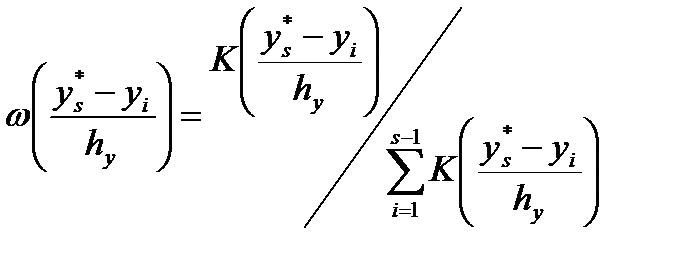 .
.
При нескольких управляющих воздействиях расчёт каждого управления проводится по формулам:
 , k=1,…,m;
, k=1,…,m;
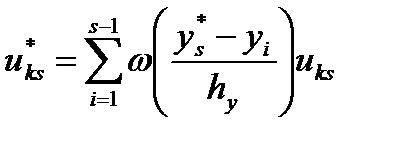 , k=1,…,m
, k=1,…,m
Дата добавления: 2015-04-18; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |