Оценка Рознблатта-Парзена (при непараметрической обработке информации).

Плотность распределения вероятности связана с функцией распределения через оператор дифференцирования

Это уравнение берём за основу при построении оценки плотности распределения вероятности. Заменяем в предыдущем уравнении производную конечной разностью:

а функции распределения , 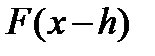- их простейшими кусочно-постоянными оценками:

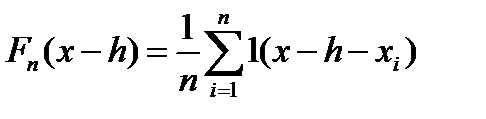построенными на основе выборки х1,…хn для одномерной случайной величины Х. Оценка плотности тогда приобретает вид

На рисунке показано, что под знак суммы этой оценки входит селектирующее прямоугольное ядро где

Ядро I(z) симметричное и площадь под кривой I(z) равна единице. Эта функция ничм не отличается от плотности распределения вероятности случайной величины z, равномерно распределённой в интервале [-1;1]. В итоге оценка для плотности распределения вероятности имеет вид

Оценка Розенблатта-Парзена по структуре совпадает с простейшей точечной оценкой только в ней дельта-функция заменена дельта-образной прямоугольной функцией .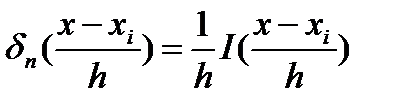

Дельта-образная прямоугольная функция имеет ширину 2h, высоту 1/2h, она расположена симметрично около точки xi. Площадь под дельта-образной функцией единичная.

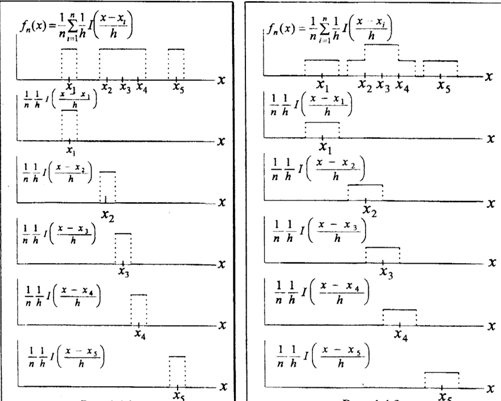
На рисунке показан простейший пример формирования оценки Розенблатта-Парзена при различной ширине h прямоугольных ядер. На каждом рисунке приведена итоговая оценка f_n(x) и все её слагаемые. С ростом h сглаживающие свойства оценки нарастают. По h для каждого конечного объёма выборки существует некоторый оптимум, ибо при малых h оценка представляет собой набор непересекающихся (или слабо пересекающихся) дельта-образных функций и оценка теряет свой смысл, а при большом h оценка становится сильно заглаженной и не отражает индивидуальных особенностей плотности распределения вероятности. Степень гладкости оценки плотности зависит от степени гладкости ядра. Заменим в оценке f_n(x) прямоугольное ядро I(z) на произвольное K(z) и получим

Здесь h – коэффициент размытости ядра. Примеры треугольного, параболического и кубического ядер приведены ниже:

Вид этих ядер изображён на рисунке. Все они нормированы на 1. В многомерном случае оценка плотности равна сумме с весом 1/n дельта-образных многомерных функций, которые можно выбрать в виде произведения одномерных дельта-образных функций: