Непараметрическая оценка регрессии

Регрессией называют первый начальный условный момент . Это некоторая усреднённая количественная зависимость между выходом и входом объекта. Регрессия удовлетворяет квадратичному критерию . Действительно, приравнивая нулю производную от функции I по искомой величине y*,

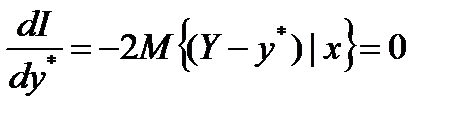и отсюда находим:подставляем в правую часть уравнения оценку условной плотности распределения вероятностей и получаем непараметрическую оценку регрессии

Оценка представляет собой выпуклую комбинацию измерений yi выхода объекта. Веса в этой выпуклой комбинации определяются входом объекта. Чем ближе значение х, для которого мы рассчитываем оценку к измерению xi, тем вес больше. Усечённость весовой функции 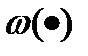позволяет при построении оценки в каждой фиксированной точке х учитывать только несколько близлежащих значений хi и не просматривать всю выборку. Выбор оптимальной формы ядра К(.) и коэффициента размытости h(.) разрешается также как и для оценок плотностей. Записывается квадратичный критерий оптимальности и из него отыскивается решение

Функция качества I от формы усечённых «колоколообразных» ядер зависит слабо. Основное влияние оказывает с. Но эта зависимость с ростом n ослабевает. Форма ядра усечённая параболическая. Константа с, определяющая коэффициент размытости, вычисляется по выборке из минимизации эмпирических функций. Если в вместо У стоит известная функция от У, например, , то по аналогии с вышерассмотренным получаем следующую непараметрическую оценку условного момента: . Для объекта с m – входами 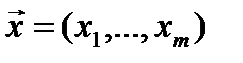и одним выходом оценка регрессии имеет следующий вид:

В оценке неизвестными являются постоянные параметры , .