
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод наименьших квадратов при линейной параметризации модели.
Модель объекта задана в виде линейной комбинации известных (базисных) функций 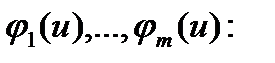
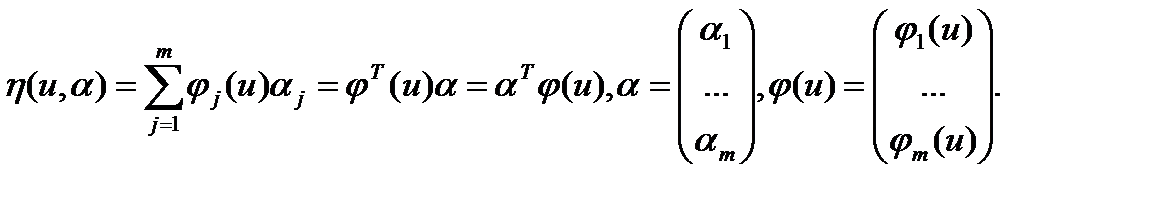
Вектор-столбец значений выхода модели (в моменты времени 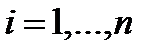 ) имеет вид
) имеет вид
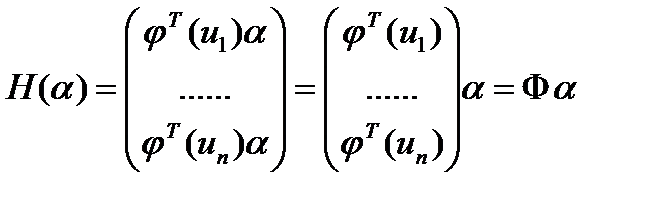 .
.
Параметры 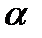 находим по критерию наименьших квадратов:
находим по критерию наименьших квадратов:

Необходимое условие минимума  (где
(где 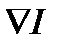 - градиент от
- градиент от 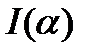 по
по  ) приводит к системе линейных алгебраических уравнений
) приводит к системе линейных алгебраических уравнений
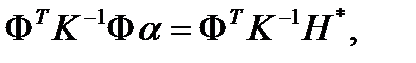 которая имеет единственное решение, если матрица
которая имеет единственное решение, если матрица  невырождена.
невырождена.
Решение системы:
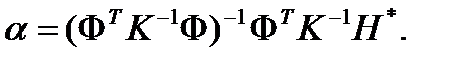
Когда помеха некоррелированна и измерения равноточные, система уравнений приобретает вид:

Этому уравнению можно придать другой вид, основанный на понятии скалярного произведения функций:

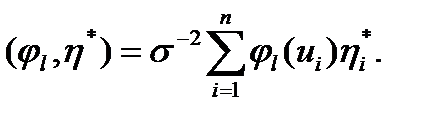
Теперь система уравнений запишется в форме:
 (1)
(1)
Если измерения выхода объекта некоррелированны, но неравноточны, то система сохраняет свой вид. Меняется лишь понятие скалярного произведения (в него вводятся веса 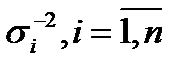 ):
):

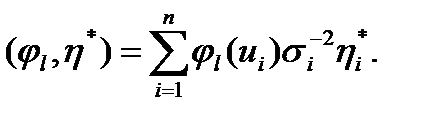
При коррелированных измерениях система также эквивалентна (1) со следующим скалярным произведением:
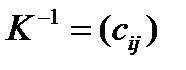 ,
,
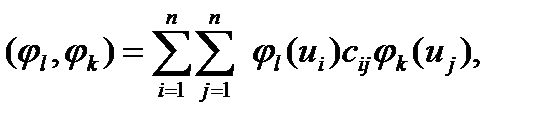

Дата добавления: 2015-04-18; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |