
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий наименьших квадратов.
Имеется объект, по измерениям 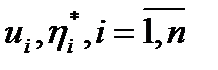 входа и выхода которого необходимо рассчитать параметры
входа и выхода которого необходимо рассчитать параметры  модели. Считаем, что выход объекта состоит из полезного сигнала
модели. Считаем, что выход объекта состоит из полезного сигнала  и центрированной помехи
и центрированной помехи 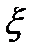 , (т. е.
, (т. е.  ). Сигнальная часть выхода представляет собой известную функцию от выхода с неизвестными параметрами
). Сигнальная часть выхода представляет собой известную функцию от выхода с неизвестными параметрами  . В структуру функции
. В структуру функции 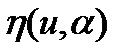 вкладывается вся априорная информация об объекте. Все, что не удается описать в объекте, относится к помехе.
вкладывается вся априорная информация об объекте. Все, что не удается описать в объекте, относится к помехе.
В зависимости от свойств помехи критерий наименьших квадратов приобретает различные формы – от простейшей до самой общей.
Если измерения некоррелированные ( т.е.  при
при  ), неравноточные критерий наименьших квадратов имеет вид:
), неравноточные критерий наименьших квадратов имеет вид:


При равноточных измерениях весовые коэффициенты  характеризующие информативность измерений , одинаковы. Тогда имеем:
характеризующие информативность измерений , одинаковы. Тогда имеем:

Если все помехи  коррелированны, т.е.
коррелированны, т.е.

То критерий наименьших квадратов базируется на элементах  матрицы , обратной корреляционной:
матрицы , обратной корреляционной:

Это общая форма критерия. Она включает все предыдущие формы.
Запишем критерий в матричном виде. Вводим обозначения:
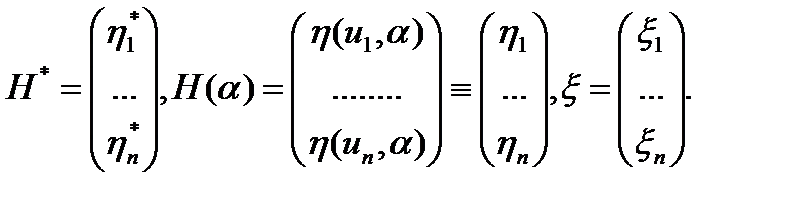
Теперь критерий наименьших квадратов приобретает вид:
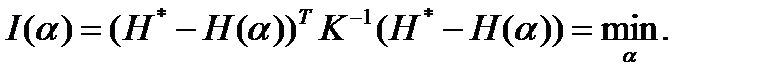
Дата добавления: 2015-04-18; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |