Последовательный симплекс метод оптимизации.

Правильный симплекс – это регулярный многогранник в c (m+1) вершинами. В двумерном пространстве правильный симплекс представляет собой равносторонний треугольник. В трёхмерном – тетраэдр. Остановимся на одном из способов построения правильного симплекса. Вначале построим симплекс, одна из вершин которого находится в начале координат. Координаты вершины определяются матрицей

.

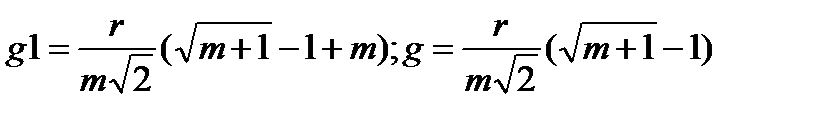в каждой строке которой расположены координаты соответствующих вершин. Ребро симплекса равно r. Для m=1, r=1. Симплексом является отрезок с координатами 0, 1. Для m=2 r=1 симплексом является правильный треугольник с координатами вершин (0;0), (0,96; 0.26), (0,26; 0,96).

Симплекс из начала координат можно переместить в любую выбранную точку пространства.

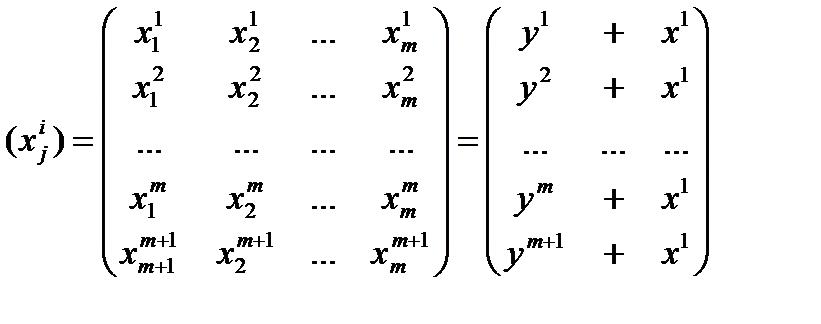
После вычисления в вершинах симплекса целевой функции находим её максимальное значение. Допустим, I(x) максимально в вершине 1.

Вершину 1 отражаем через центр противоположной грани и получаем симплекс с вершинами 2,3,4. В вершине 4 вычисляем I(x). Дальнейшие шаги повторяются. Формализуем их.

1. Задаётся исходная вершина симплекса , размер r симплекса и строится симплекс.

2. В вершинах симплекса вычисляется минимизируемая функция .

3. Осуществляется проверка выполнения условий окончаний поиска оптимума . Поиск завершается, когда или размеры симплекса или разности между значениями функции в вершинах становятся достаточно малы. Можно требовать и одновременно выполнения двух условий этого пункта. При выполнении условия процесс поиска заканчивается. Решением задачи (с выбранной точностью) является точка х1, I(x1) – точка с минимальным значением функции I(x). Если неравенство не выполняется, то осуществляется перемещение к оптимуму за счёт перехода одного симплекса к другому.

4. Находится наихудшая вершина симплекса. Это вершина с максимальным значением I(x). 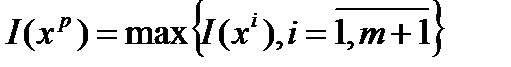. Вычисляется центр тяжести противоположной грани: .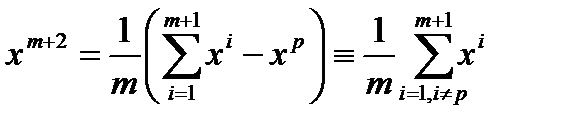

5. Осуществляется отражение вершины x 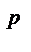относительно х: и в точке 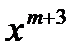вычисляется функция .

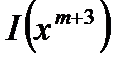6. Если точка 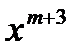оказывается хуже всех остальных точек нового симплекса, то осуществляется возврат к прежнему симплексу с последующим его сжатием относительно лучшей из вершин х1. симплекса: , , 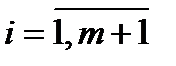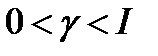. Здесь 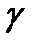- коэффициент сжатия симплекса. Осуществляется переход к шагу 2. Если же точка 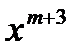не является худшей в новом симплексе, то продолжается дальнейшее движение (переход к шагу 4).