Применение непараметрического сглаживания в классификации ( в распознавании образов)

Для простоты рассматриваем случай двух классов 1, 2 и проблему восстановления решающей функции по обучающей выборке х₁, … , х_n, которая состоит из двух подвыборок: x_i, , когда истинным является класс 1, x_i, , когда истинным является класс 2.

Объёмы этих подвыборок n1 и n2, причём n1+n2 = n. Принадлежность выборочных значений тому или иному классу можно характеризовать новой переменной:

В пространстве переменных (х,у) на базе указанных экспериментальных точек строится решающая функция в виде непараметрической оценки регрессии: .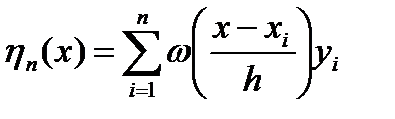

Решающее правило на базе её, как известно, имеет вид:

если , то принимается решение об истинности класса 1;

если , то принимается решение об истинности класса 2.

Параметр с коэффициента размытости находим по экзаменующей выборке (которая также состоит из двух подвыборок, принадлежность которым характеризуется переменной , введённой на базе экстремального критерия, например: .

В многомерном случае (когда имеется несколько информативных признаков) схема решения не меняется. В этом случае колоколообразная нормированная весовая функция зависит от всех информативных признаков, а по критерию, приведённому выше, ведётся настройка нескольких параметров. Настройку параметров с коэффициентов размытости h можно проводить, используя ту же обучающую выборку. При этом все точки выборки попеременно участвуют в обучении и в экзамене. В точке x_j непараметрическая решающая функция строится с учётом всех точек (вернее только тех точек, которые охватывает колоколообразная нормированная функция 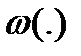обучающей выборки за исключением выборочной точки :

.

Точка ( ), не участвовавшая в построении решающей функции, используется в критерии настройки с. Например,

.