Билет 19. Методы одномерного поиска минимума унимодальных функций.

Методы одномерного поиска минимума унимодальных функций.

Рассмотрим вначале самый простой случай, когда оптимизация ведётся только по одной переменной, т.е. унимодальной функцией. Например, после того, как найдено направление поиска (в пространстве многих переменных), оптимизация вдоль этого направления представляет собой оптимизацию относительно одной переменной.

Имеется функция одной переменной. Необходимо найти её минимум при х, изменяющемся в интервале [a,b]: I(x)=min.

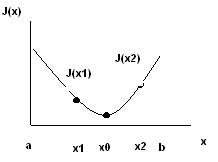
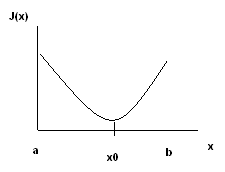
Непрерывная функция I(x) с минимумом является унимодальной на интервале [a,b], если существует такая точка x⁰ принадлежит [a,b], что на отрезке [a,x⁰] функция I(x) убывает, а на отрезке [x⁰,b] возрастает. Основное свойство унимодальной функции, используемое в методах поиска её минимума, состоит в том, что вычисление любых двух значений I(x1), I(x2) из интервала [a,b] (причём х1х2) позволяет уменьшить интервал локализации точки минимума x0. Можно убедиться, если I(x1) < I(x2), где х1<х2, то х0 принадлежит [a,x2]. Если же I(x1)>I(x2), где х1<х2, то х0 принадлежит [x1,b].