
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тест по матлогике для проведения экзамена в группах 1211,1212- июнь 2010 год.
1. КНФ – это:
a) дизъюнкция элементарных конъюнкций;
b) дизъюнкция любого числа переменных;
c) конъюнкция элементарных дизъюнкций;
d) конъюнкция переменных или их отрицаний;
2. Конъюнкцией двух высказываний P и Q называется высказывание,
a) ложное в случае, когда оба высказывания ложны, и истинное – во всех других случаях;
b) истинное, когда истинностные значения P и Q совпадают, и ложное – в противном случае;
c) истинное, когда оба высказывания истинны, и ложное – во всех других случаях;
d) ложное, когда Р истинно, а Q ложно; во всех других случаях – истинное;
3. Как называется логическая операция, которая обозначается знаком  ?
?
a) неравнозначность;
b) эквивалентность;
c) импликация;
d) инверсия;
4. Найти эквивалентные формулы:
1)  1)
1) 
2)  2)
2) 
3)  3)
3) 
4)  4)
4) 
5. Какой знак следует поставить вместо «?» в данной таблице истинности?
| A | B | A?B |
a)  ;
;
b) │ ;
c) → ;
d)  ;
;
6. Законы де-Моргана:
a)  ,
,
 ;
;
b)  ,
,
 ;
;
c)  ,
,
 ;
;
d)  ,
,
 ;
;
7. Какая из этих схем является схемой неправильных рассуждений?
a)  ;
;
b)  ;
;
c)  ;
;
d)  ;
;
8. Количество входных наборов m булевой функции n переменных, или область определения булевой функции, вычисляется по формуле:
a)  ;
;
b)  ;
;
c)  ;
;
d)  ;
;
9. Совершенной ДНФ (СДНФ) называется
a) ДНФ, каждая элементарная конъюнкция которой включает все переменные с отрицанием или без;
b) логическая сумма любого числа переменных булевой функции, взятых с отрицанием или без;
c) КНФ, каждая элементарная дизъюнкция которой содержит все переменные с отрицанием или без;
d) произведение любого числа переменных булевой функции, взятых с отрицанием или без;
10. Основной формой мышления не является:
a) понятие;
b) обсуждение;
c) умозаключение;
d) высказывание;
11. Термин «нормальная» в словосочетании «конъюнктивная нормальная форма» означает, что
a) переменные взяты с отрицанием или без;
b) в данном выражении отсутствуют групповые инверсии, т.е. инверсия над несколькими переменными сразу;
c) в выражении нет одинаковых элементарных дизъюнкций;
d) каждая дизъюнкция содержит все переменные данной булевой функции;
12. Какое из этих предложений является высказыванием?
a) Рим – столица Франции.
b) Который час?
c) Решить уравнение x2+3x-2=0.
d) Вперед, Россия!
13. Если функция задается в виде алгебраического выражения, получаемого путем применения каких-либо логических операций к переменным алгебры логики, то это следующий способ представления логических функций:
a) аналитический;
b) координатный;
c) числовой;
d) словесный;
14. Импликация – это:
a) логическое произведение;
b) логическая сумма;
c) сложение по модулю 2;
d) логическое следование;
15. Выражению  эквивалентно выражение:
эквивалентно выражение:
a)  ;
;
b)  ;
;
c)  ;
;
d)  ;
;
16. Если из А и В следует С, то из А и не С следует не В – это:
a) Правило сечения;
b) Правило контрапозиции;
c) Правило сложной контрапозиции;
d) Правило импортации;
В нижеприведенных заданиях провести соответствия между выражениями в левом и правом столбцах:
17.
1)  1) Правило отрицания
1) Правило отрицания
2)  2) Правило утверждения – отрицания
2) Правило утверждения – отрицания
3)  3) Утверждающий модус
3) Утверждающий модус
4)  4) Правило отрицания – утверждения
4) Правило отрицания – утверждения
18.
1)  1) Правило отрицания – утверждения
1) Правило отрицания – утверждения
2)  2) Транзитивность
2) Транзитивность
3)  3) Закон противоречия
3) Закон противоречия
4)  4) Правило контрапозиции
4) Правило контрапозиции
19.
1)  1) Правило сложной контрапозиции
1) Правило сложной контрапозиции
2)  2) Правило сечения
2) Правило сечения
3)  3) Правило импортации
3) Правило импортации
4)  4) Правило экспортации
4) Правило экспортации
20.
1)  1) Закон «исключения третьего»
1) Закон «исключения третьего»
2) 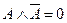 2) Закон двойного отрицания
2) Закон двойного отрицания
3)  3) Закон не противоречия
3) Закон не противоречия
4)  4) Закон тождества
4) Закон тождества
21.
1)  1) Закон коммутативности
1) Закон коммутативности
2)  2) Законы де-Моргана
2) Законы де-Моргана
3)  3) Закон ассоциативности
3) Закон ассоциативности
4)  4) Закон дистрибутивности
4) Закон дистрибутивности
22. Как называются следующие знаки:
1)  1) Импликация
1) Импликация
2) ↓ 2) Штрих Шеффера
3) → 3) Стрелка Пирса
4)│ 4) Сложение по модулю 2
23.
1) Правило отрицания-утверждения 1) Если из А следует и В, и не В, то неверно А
2) Закон противоречия 2) Если из А и В следует С, то из А и не С следует не В
3) Правило сложной контрапозиции 3) Если из А следует В, а из В и С следует Д, то из А и С следует Д
4) Правило сечения 4) Если истина А или В (в неразделительном смысле) и неверно одно из них, то другое – истинно
24.
1) Понятие 1) форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)
2) Высказывание 2) форма мышления, фиксирующая основные существенные признаки объекта
3) Умозаключение 3) наука о формах и способах мышления
4) Логика 4) форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними
25.
1) Конъюнкция 1) высказывание, истинное, когда истинностные значения P и Q совпадают, и ложное – в противном случае
2) Дизъюнкция 2) высказывание, истинное, когда оба высказывания истинны, и ложное – во всех других случаях
3) Импликация 3) высказывание, ложное в случае, когда оба высказывания ложны, и истинное – во всех других случаях
4) Эквивалентность 4) высказывание, ложное, когда Р истинно, а Q ложно; во всех других случаях – истинное
26. Провести соответствие между логическими операциями и их таблицами истинности
1) Неравнозначность 2) Эквивалентность 3) Дизъюнкция 4) Импликация
1) 2) 3) 4)
| x | y | f |
| x | y | f |
| x | y | f |
| x | y | f |
27.
1) Элементарная конъюнкция 1) формула, имеющая вид дизъюнкции элементарных конъюнкций
2) КНФ 2) дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза
3) Элементарная дизъюнкция 3) конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза
4) ДНФ 4) конъюнкция элементарных дизъюнкций
28. К каким схемам относятся следующие рассуждения:
1) Если рабочий отсутствовал на 1) 
работе, он не выполнил задание. Он не
выполнил задание. Следовательно, он
отсутствовал на работе.
2) Этот человек студент или 2) 
предприниматель. Он студент.
Следовательно, не предприниматель.
3) Этот человек постоянно живет в 3) 
Москве или в Санкт-Петербурге. Он
живет в Москве. Следовательно, он
не живет в Санкт-Петербурге.
4)Сегодня понедельник или вторник. 4) 
Сегодня вторник. Следовательно,
сегодня не понедельник.
29. Способы представления логических функций:
1) Графический 1) функция задается в виде таблицы истинности, которая содержит 2n строк по числу наборов аргументов, n столбцов по числу переменных и один столбец значений функции
2) Координатный 2) является способом представления функционирования схемы, реализующей булеву функцию во времени
3) Табличный 3) функция задается в виде n-мерного единичного куба, вершинам которого соответствуют наборы значений аргументов и приписаны значения функции на этих наборах
4) Диаграммный 4) таблица истинности функции представляется в виде координатной карты состояний, которая часто называется картой Карно
30. Пусть предикат P(x; y) описывает отношение людей “x любит y” на множестве людей. Рассмотрите следующие варианты навешивания кванторов:
1)  P(x; y) 1) Существует человек, который кого-то любит
P(x; y) 1) Существует человек, который кого-то любит
2)  P(x; y) 2) Существует человек, который любит всех людей
P(x; y) 2) Существует человек, который любит всех людей
3)  P(x; y) 3) Все люди любят всех людей
P(x; y) 3) Все люди любят всех людей
4) 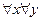 P(x; y) 4) Всякий человек кого-нибудь любит
P(x; y) 4) Всякий человек кого-нибудь любит
Открытые тестовые задания.
31. __________ двух высказываний P и Q называется высказывание, истинное, когда истинностные значения P и Q совпадают, и ложное – в противном случае.
32. __________– это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.
33. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются __________.
34. __________ – это функция, принимающая значения 0 и 1, аргументы которой также принимают значения 0 и 1.
35. Формулы называются __________, если они представляют одну и ту же функцию.
36. Алгебра, образованная бинарным множеством В={0,1} вместе со всеми возможными операциями на нем, называется __________.
37. Буквы, обозначающие высказывания, логические связки и скобки составляют __________ языков логики высказываний.
38. Высказывание является __________ тогда, когда оно не соответствует реальной действительности.
39.Если функция задается в виде n-мерного единичного куба, вершинам которого соответствуют наборы значений аргументов и приписаны значения функции на этих наборах, то это __________
способ представления функции.
40. Формула 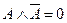 отражает содержание закона __________.
отражает содержание закона __________.
41. Способ представления функционирования схемы, реализующей булеву функцию во времени, называется __________.
42. Если некоторые переменные входят под знаком кванторов, стоящих перед предикатом, то они называются __________ переменными, остальные переменные называются __________.
43. Выражение, на которое навешивается квантор, называется __________ квантора.
44. Множество всех единичных наборов называется __________ функции f.
45. Высказывание, в котором связь понятий правильно отражает свойства и отражение реальных вещей называется __________.
Дата добавления: 2015-04-21; просмотров: 273; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Дела по экономическим спорам и другие дела, связанные с осуществлением предпринимательской и иной экономической деятельности; | | | Структура бухгалтерського балансу |