
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение Чарномского. Расчет кривых в естественных руслах.
РИСУНОК (стр. 237, Константинов)
Составим уравнение Бернулли для сечений 1—1 и 2—2 относительно
выбранной плоскости сравнения О2—О2,: Э+i0Δl=Э+Δ hf. После приведения: i0Δl = ΔЭ + Δhf.
На участке между сечениями 1—1 и 2—2 движение жидкости является плавноизменяющимся, поэтому энергия потока расходуется на преодоление сопротивлений по длине, а потери энергии на местные сопротивления можно считать пренебрежимо малыми, т. е. Δhf=Δht. Отношение потерь напора к длине участка является средним значением гидравлического уклона на участке:
 , тогда
, тогда  или
или  .
.
Для непризматических русл с уклонами дна i0=O и i0<0 уравнение  и
и 
Уравнения записаны в конечных разностях. В такой форме они впервые были приведены В. И. Чарномским.
При бесконечно малом расстоянии dl между сечениями 1—1 и 2—2 можно получить уравнения в дифференциальной форме:  ,
,  ,
, 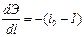
Дата добавления: 2015-04-18; просмотров: 368; Мы поможем в написании вашей работы!; Нарушение авторских прав |