
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действующее значение несинусоидальной величины.
Действующим называют значение несинусоидального тока, эквивалентное постоянному току по тепловому действию.
При этом нужно учесть, что несинусоидальный ток складывается из постоянной составляющей и ряда гармоник:
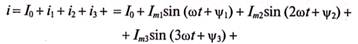
Каждая составляющая несинусоидального тока выделяет тепло в некотором элементе цепи с сопротивлением R. Воспользовавшись рассуждениями § 10.3 для определения действующих значений тока гармоник и постоянной составляющей несинусоидального тока, можно сделать вывод, что
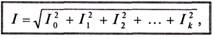 (18.19)
(18.19)
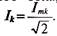 где /0 — постоянная составляющая несинусоидального тока; I1, I2, Ik, — действующее значение токов гармоник, т.е.
где /0 — постоянная составляющая несинусоидального тока; I1, I2, Ik, — действующее значение токов гармоник, т.е.
Таким образом, действующее значение несинусоидального тока является средней квадратичной величиной постоянной составляющей и действующих значений токов гармоник.
С учетом выражения (10.9) действующее значение несинусоидального тока можно определить по формуле
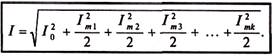 (18.20)
(18.20)
Аналогично действующее значение несинусоидального напряжения определяется выражением
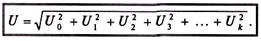 (18.21)
(18.21)
Действующее значение несинусоидального напряжения является средней квадратичной величиной постоянной составляющей и действующих значений напряжений гармоник.
Действующие значения несинусоидальных токов и напряжении измеряются амперметрами и вольтметрами электромагнитной, электродинамической и тепловой систем.
Кроме коэффициента формы Кф и коэффициента амплитуды Kа, определение которых дано в §10.3 (выражение (10.10) и (10.11)), несинусоидальные периодические кривые характеризуются коэффициентом искажений КИ. Коэффициент искажений определяется отношением действующего значения основной (первой) гармоники тока или напряжения к действующему значению этих несинусоидальных величин. Такое определение аналогично 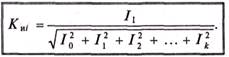 для ЭДС, магнитного потока и т. д. Г Коэффициент искажения тока
для ЭДС, магнитного потока и т. д. Г Коэффициент искажения тока
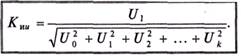 Коэффициент искажения напряжения
Коэффициент искажения напряжения
(18.23)
Для синусоиды КИ=1.
Чем меньше коэффициент искажения отличается от единицы, тем ближе к синусоиде данная кривая.
Так,например, для треугольной формы кривой (кривая 2 таблицы 18.1) - Ки≈0,99, а для прямоугольной формы кривой (кривая 3 таблицы 18.1) - КИ≈0,9.
( В электронике и радиотехнике несинусоидальность кривой характеризуют коэффициентом гармоник, показывающим удельный вес высших гармоник Кr относительно первой (основной) гармоники:
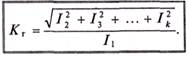 (
(
Чем меньше коэффициент гармоник, тем ближе к синусоиде Несинусоидальная кривая.
16. 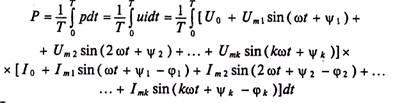 Мощность несинусоидального тока.
Мощность несинусоидального тока.
Под активной мощностью Р несинусоидального тока понимают среднее значение мгновенной мощности (§ 11.1) за период, т. е.
Проинтегрировав это выражение, получают
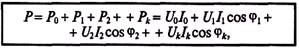 (18.25)
(18.25)
где Ро — мощность постоянной составляющей несинусоидального тока; P1, Р2, , Рk — активные мощности гармоник несинусоидального тока.
Таким образом, потребляемая, т. е. активная, мощность в цепи несинусоидального тока определяется суммой постоянной мощности и активных мощностей гармоник.
Реактивная мощность в цепи несинусоидального тока, по аналогии, определяется выражением
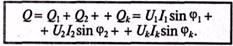 (18.26)
(18.26)
Реактивная мощность в цепи несинусоидального тока определяется суммой реактивных мощностей гармоник.
Постоянная составляющая реактивной мощности отсутствует, так как для постоянного тока колебание мощности (энергии) немыслимо.
Полная, или кажущаяся, мощность в цепях несинусоидального тока равна S=UI.
Следует иметь в виду, что несинусоидальный ток или напряжение не могут быть выражены при помощи векторов. Кривые несинусоидального тока и напряжения в общем случае даже не подобны. Так что невозможно применить понятие об угле сдвига фаз, принятое для синусоидальных токов.
Поэтому при изучении некоторых свойств цепей несинусоидального тока несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными. Замена производится таким образом, что действующее значение синусоидального тока принимается равным действующему значению заменяемого несинусоидального тока, а действующее значение синусоидального напряжения принимается равным действующему значению несинусоидального напряжения.
Тогда угол сдвига фаз Ф между эквивалентными синусоидами напряжения и тока выбирается таким, чтобы активная мощность эквивалентного синусоидального тока была равна активной мощности несинусоидального тока, т. е. 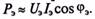
Откуда  (18.27)
(18.27)
При этом 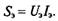 Однако для цепи несинусоидального тока
Однако для цепи несинусоидального тока
в общем случае 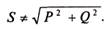 (18.28)
(18.28)
Равенство 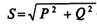 (выражение (12.14)), выведенное из треугольника мощностей (рис.12.2в), справедливо для синусоидального тока определенной частоты ώ. Несинусоидальный ток складывается из нескольких синусоидальных составляющих с разными (кратными) частотами и разными углами сдвига фаз φ между током и напряжением (определенными для каждой гармоники); т. е. для несинусоидального тока нельзя построить векторную диаграмму и прямоугольный треугольник мощностей. Поэтому выражение (12.14) для несинусоидального тока несправедливо и полная (кажущаяся) мощность не равна
(выражение (12.14)), выведенное из треугольника мощностей (рис.12.2в), справедливо для синусоидального тока определенной частоты ώ. Несинусоидальный ток складывается из нескольких синусоидальных составляющих с разными (кратными) частотами и разными углами сдвига фаз φ между током и напряжением (определенными для каждой гармоники); т. е. для несинусоидального тока нельзя построить векторную диаграмму и прямоугольный треугольник мощностей. Поэтому выражение (12.14) для несинусоидального тока несправедливо и полная (кажущаяся) мощность не равна 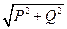
Дата добавления: 2015-04-21; просмотров: 424; Мы поможем в написании вашей работы!; Нарушение авторских прав |