Мощность в комплексном виде

§ Для неразветвленной цепи с Я и С (рис. 12.3а) мгновенные зна­чения тока и напряжения можно записать как

Комплексы напряженияi тока соответственно равны

Комплекс полной мощности цепи S определяется произве­дением комплекса напряжения U и сопряженного комплекса тока (над сопряженным комплексом синусоидальной величины ставят «звёздочку»")

(14.10)

Таким образом, модулем комплекса полной мощности S являет­ся кажущаяся мощность цепи S=UI, а аргументом — угол сдвига фаз между током и напряжением.

Если комплекс полной мощности S перевести из показатель­ной формы в алгебраическую, то получится

(14.11)

То есть вещественная часть комплекса полной мощности — ак­тивная мощность Р, а коэффициент при мнимой единице — реак­тивная мощность Q.

Знак перед поворотным множителем j указывает на характер Цепи. В рассматриваемой цепи реактивная мощность емкостно­го характера

Комплексы величин токов, напряжений, сопротивлений, мощ­ностей и других параметров цепи синусоидального тока необхо­димо выражать в двух видах записи комплексного числа: показа­тельной и алгебраической. В этом случае сразу определяются Действующие значения тока, напряжения, кажущееся сопротив­ление, его активные и реактивные части (R и X), угол сдвига фаз ср Между током и напряжением, характер цепи, кажущаяся S, актив­ная Р и реактивная Q мощности. Кроме того, в неразветвленной цепи напряжения на участках складываются, суммируются токи в разветвленных цепях, а сложение комплексов можно производить только в алгебраической форме записи. В алгебраической форме записи кажущейся мощности S сразу определяются активная мощность Р и реактивная мощность Q. В показательной форме записи сопротивлений производится их умножение и деление, необходимое при расчете цепей синусоидального тока при сме­шанном соединении потребителей, и т.д. Необходимость выра­жения комплексов в двух видах следует из примеров, разобран­ных в этой главе.

4. Вращающееся магнитное поле трёхфазного тока.

Вращающееся магнитное поле трехфазного тока

Получение вращающегося магнит­ного поля рассматривается на примере магнитного поля трехфазного тока.

Если по трем неподвижным одинаковым катушкам (обмоткам) АХ, BY и CZ, скрепленным под углом 120° в пространстве (рис. 17.1), пропустить трехфазный ток (рис. 17.2)

;

то в этих обмотках создается трехфазный магнитный поток

(рис. 17.2)

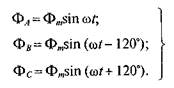(17.2)

На рис. 17.1 и 17.2 обмотки изображены упрощенно, каждая в виде одного витка с началами А, В, С и концами соответственно X, Y, Z

Трехфазный магнитный поток внутри этих неподвижных катушек создает вращающееся магнитное поле трехфазного тока ^!|(рис. 17.2).

За положительное направление тока в обмотках принято направление от начала каждой катушки к ее концу, как показано на рис. 17.1.

Направление магнитного потока, созданного тремя обмотками для моментов времени а, Ь, с, c, d, е, определяется по временной диаграмме (рис. 17.2) в зависимости от направления тока в каж­дой обмотке в эти моменты времени.

Направление магнитного потока, созданного каждой активной стороной обмотки (и их сочетанием), определяется по правилу буравчика для каждого момента времени. Направление суммар­ного потока Ф для каждого момента времени показано на рис. 17.2 прямыми стрелками Ф.

Как видно, магнитное поле Ф внутри неподвижных обмоток вращается по часовой стрелке. Для изменения направления вращения магнитного поля достаточно изменить чередования фаз обмоток при подключении последних к трехфазной цепи (на­пример, поменять местами подключение двух обмоток: ВС и СА).

Величина вращающегося магнитного потока Ф остается посто­янной и равной Ф= 1,5Ф_m одной фазы, что можно наблюдать по временной диаграмме в любой момент времени (рис. 17.2). Вращающееся магнитное поле трехфазного тока нашло широко, применение в трехфазных машинах (асинхронных и синхронных).