Ток, напряжение и сопротивление в комплексном виде

Если ток и напряжение изменяются по синусоидальному зако­ну то, как указывалось выше их можно изобразить векторами и, следовательно, записать комп­лексными числами:

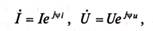(14.6)

где - комплексы тока и напряжения. Точка над комплексами указывает, что ток и напряжение изменяются по синусо­идальному закону с определенной частотой ώ; I и U — модули i комплексов тока и напряжения, они же действующие значения

тока и напряжения — аргументы комплексов тока и напряжения, они же начальные фазы тока ψ_i и на­пряжения ψ_u.

Для неразветвленной цепи с R и L (рис. 12.1а) мгновенные зна­чения синусоидального тока и напряжения можно записать так:

Тогда комплексы тока и напряжения

(14.7)

Комплекс полного сопротивления цепи Z определяется отно­шением комплекса напряжения к комплексу тока, т. е.

(14.8)

Комплексные величины, не зависящие от времени, обознача­ются прописными буквами с черточкой внизу. Модулем комплекса полного сопротивления является кажущееся

сопротивление цепи 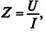а аргументом — угол сдвига фаз между током и напряжением φ.

Алгебраическая форма записи комплекса полного сопротивле­ния Z

(14.9)

Вещественная часть комплекса полного сопротивления есть ак­тивное сопротивление R, а коэффициент при мнимой единице j " реактивное сопротивление X. Знак перед поворотным множите­лем (мнимой единицей) указывает на характер цепи. Знак «плюс» соответствует цепи индуктивного характера, а знак «минус» - цепи емкостного характера.

Выражения комплексов сопротивлений различных цепей при­ведены в Приложении 7.

Обратная величина комплекса сопротивления — комплекс про­водимости

Любую цепь переменного тока можно рассчитывать по зако­нам постоянного тока, если все величины представить в комплек­сной форме. В этом и заключается достоинство символического метода расчета.