Действия над комплексными числами

Действия над комплексными числами.

Действия над комплексными числами

Символический метод нашел широкое применение для расчета сложных цепей переменного тока.

Символический метод расчета основан на использовании комп­лексных чисел.

Комплексное число А состоит из вещественной А и мнимой А" частей, т.е.

A = A+jA".

Комплексное число на комплексной плоскости можно предста­вить вектором. Проекция вектора на вещественную ось (ось абсцисс) соответствует вещественной части комплексного числа А (рис. 14.1а). Проекция вектора на мнимую ось у (ось ординат) со­ответствует коэффициенту при мнимой единице А". Мнимая еди­ница у представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки, т.е. в положительном направлении. Мнимая единица j = √-1. Тогда j² = -1; j³ = -j; j⁴ = 1.

Комплексным числам A = 3+4j и B = 5-2j соответствуют век­торы А и В, изображенные на комплексной плоскости (рис. 14.1а и б) в масштабе.

Модуль комплексного числа соответствует длине вектора, изоб­ражающего это комплексное число.

Из построения (рис. 14.1а) видно, что модули комплексных чисел определяются выражением

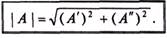(14.1)

Следовательно,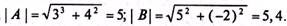

Углы ά и β, образованные векторами А и В с положительным направлением вещественной оси, называются аргументами комп­лексного числа.

Аргументы комплексного числа (рис. 14.1а) определяются вы­ражением

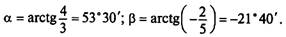
(14.2)

То есть

Как видно, аргумент комплексного числа В отрицательный, так как вектор В повернут на угол β по часовой стрелке, а не против.

Существует три формы записи комплексного числа:

1) алгебраическая: 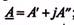; (14.3)

2) тригонометрическая: (14.4)
так как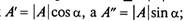

3) показательная:

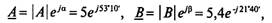(14.5)

где е — основание натурального логарифма, однако в данном случае имеет чисто символическое значение.

Для перевода из показательной формы записи комплексного числа в алгебраическую пользуются тригонометрической формой записи комплексного числа (14.4).

Для перевода из алгебраической формы записи комплексного числа в показательную определяют модуль по (14.1) и аргумент по (14.2) комплексного числа.

Для перевода комплексного числа из одной формы в другую можно использовать логарифмическую линейку или микрокаль­кулятор.

Комплексные числа можно складывать, вычитать, умножать и делить.

Сложение и вычитание комплексных чисел производится толь­ко в алгебраической форме

На рис. 14.16 видно, что сложение и вычитание комплексных чисел соответствует сложению и вычитанию векторов, изобра­жающих эти числа.

Умножение и деление комплексных чисел можно производить в алгебраической форме:

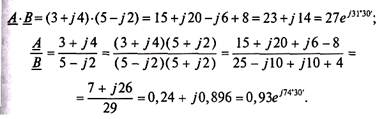
Для того чтобы избавиться от комплексов в знаменателе, чис­литель и знаменатель умножают на комплекс, сопряженный с комплексом знаменателя. У сопряженного комплекса знак перед мнимой единицей j изменяется на обратный.

Произведение двух сопряженных комплексов — вещественное число, равное сумме квадратов вещественной и мнимой частей этих комплексов.

Однако умножение и деление комплексных чисел удобно про­изводить в показательной форме.

При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются алгебраически:

При делении комплексных чисел в показательной форме моду­ли этих чисел делятся, а аргументы вычитаются с учетом знаков:

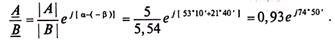
Таким образом, сложение и вычитание комплексных чисел можно производить только в алгебраической форме, а умножение и де­ление удобней и проще производить в показательной форме.