Идея динамического программирования (ДП)

Метод ДП (Р. Беллман, В.С. Михалевич, Н.З. Шор ) можно трактовать как алгоритмическую версию рассуждений по индукции.

Пусть s_k(y), 1 £ k £ n, 0 £ y £ Y, — оптимальное значение целевой функции задачи (1) – (3), где n заменено на k, Y заменено на y.

Требуется найти s_n(Y) и набор переменных, на котором достигается это значение.ТЕОРЕМА 1.Пусть f₁, … , f_n ­—монотонно неубывающие функции. Тогда справедливы следующие рекуррентные соотношения:

s1(y) = f1(y), 0 £ y £ Y;	(4)
sk(y) = max {sk-1(y - x) + fk(x) | 0 £ x £ y}, 2 £ k £ n, 0 £ y £ Y,	(5)

Доказательство:Соотношение (4)очевидно. По определению

s_k(y) ³ max {s_k-1(y - x) + f_k(x) | 0 £ x £ y}.

Пусть теперь — такой вектор, что и

.

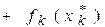Поскольку имеем

. Алгоритм ДП вычисляет множество S_k ={s_k(y) | 0 £ y £ Y}, k =1,…,n с помощью соотношений (4) и (5), где на каждом шаге оптимизируется ровно одна переменная.

Процесс вычисления S1,…,Sn называется прямым ходом алгоритма. Число операций » Y 2n Память » Y n .

y S1(y) S2(y) … Sn(y)                                 Y       Sn(Y)

При обратном ходе алгоритма вычисляются значения 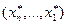, с учетом того, что уже известны S_k(y). Например, определяется из уравнения 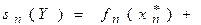и так далее.

Число операций » Y n. Память » Y Характеристики алгоритмов

 

Для оценки качества алгоритмов будем использовать два параметра:

T_A— трудоемкость (число элементарных операций алгоритма A);

П_А — требуемый объем памяти.

Элементарная операция — одна из арифметических операций: сложение, вычитание, умножение, деление или логическая операция сравнение двух чисел.

Нас будет интересовать зависимость параметров алгоритма от длины записи исходных данных задачи с точностью до порядка величин.

Пример: При Т = 3/2 n² , будем писать T = O(n²) или T » n².