
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полиномиальные алгоритмы
Определение. Алгоритм A называют полиномиальным, если его трудоемкость TA ограничена полиномом от длины записи исходных данных, то есть существует константа c > 0 и натуральное число k такие, что TA £ c Lk, где L — длина записи исходных данных.
Пример: Пусть fi (xi) = ai xi, тогда 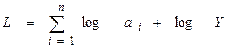 ,
,
но TДП = O(Y2n), то есть алгоритм ДП не является полиномиальным.
Обобщим задачу (1)–(3):
| f1(x1) +…+ fn(xn) ® max | (1¢) |
| h1(x1) +…+ hn(xn) £ Y | (2¢) |
| ai ³ xi ³ 0, целые, i = 1,…n. | (3¢) |
Если hi(x) — целочисленные монотонно неубывающие функции, то вместо (4)–(5) можно использовать следующие рекуррентные соотношения:
| s1(y) = f1(x* ), где x* = max{x £ a1 | h1(x) £ y}, 0 £ y £ Y; | (4¢) |
sk(y) = 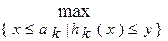 { fk(x) + sk-1(y - hk(x))}, 2 £ k £ n, 0 £ y £ Y. { fk(x) + sk-1(y - hk(x))}, 2 £ k £ n, 0 £ y £ Y.
| (5¢) |
Упражнение 1. Доказать справедливость соотношений (4¢)–(5¢).
Обратная задача — поиск наименьших затрат на получение заданного количества продукции:
| h1(x1) +…+ hn(xn) ® min | (6) |
| f1(x1) +…+ fn(xn) ³ D | (7) |
| ai ³ xi ³ 0, целые, i = 1,…n. | (8) |
Если fk(x) — целочисленные монотонно неубывающие функции, то для решения задачи (6)–(8) можно использовать идеи динамического программирования.
Пусть 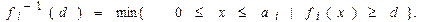
Для 1£ k £ n, 0 £ d £ D обозначим через tk(d) — оптимальное решение задачи (6)–(8), в которой n заменено на k, а D заменено на d.
Требуется найти tn(D).
 0 £ d £ D, 0 £ d £ D,
| (9) |
tk(d) = min{tk–1(d – fk(x)) + hk(x)| 0 £ x £ ak, x £ 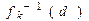 },
k ³ 2, 0 £ d £ D. },
k ³ 2, 0 £ d £ D.
| (10) |
Рекуррентные соотношения
Упражнение 2. Доказать справедливость соотношений (9)–(10).
ТЕОРЕМА 2:Предположим, что D — наибольшее число, для которого оптимальное значение целевой функции задачи (6)–(8) не превосходит Y. Тогда оптимальное значение целевой функции задачи (1¢)–(3¢) равно D.
Доказательство: Пусть D удовлетворяет условию теоремы
и 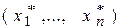 — соответствующее решение задачи (6)–(8).
— соответствующее решение задачи (6)–(8).
Значит
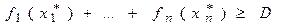 и
и 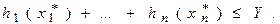
Следовательно, D не превосходит оптимального решения D1 задачи (1¢)–(3¢). Если бы D1 было больше D, то решение задачи (6)–(8), в которой D заменено на D1, тоже не превышало бы Y, что противоречит максимальности D.
Дата добавления: 2015-04-21; просмотров: 241; Мы поможем в написании вашей работы!; Нарушение авторских прав |